Chapter 2 理论与公式

本章节尚未完成，有关内容可以参考我们已经发表的文献，有详细阐述。 也可以从源代码中解读。

2.1 流域水循环

流域中水文循环基本框架，包含了高寒冰冻圈要素、地表水、地下水以及河流水文过程。
流域中水文循环基本框架，包含了高寒冰冻圈要素、地表水、地下水以及河流水文过程。

2.2 建模思路

2.2.1 水量平衡

水量平衡(或称为物质守恒)是水文模型的基础，可以简单总结为，流域系统内水储量变化要等于输入系统的水量与从系统重输出的水量之差，即ΔS=Qin−QoutΔS=Qin−Qout， 式中，ΔSΔS为计算单位的水储量，QinQin为输入水量之和，QoutQout为输出水量之和。在不同的流域单元数，都遵守这个基本物质守恒原理，但具体的输入输出量的含义、方向、量级都有不同表现。

2.2.1.1 流域水量平衡

在流域尺度最简单的水量平衡总结为：

ΔS=P−E−QΔS=P−E−Q

式中，ΔSΔS为计算单位的水储量，PP为计算单元中的降水量，EE为蒸散发总量, QQ则为从流域河流的出口流出的径流总量。

这个流域水量平衡公式貌似简单，但它有很多变幻形式，往往是初学者难以掌握或者容易出错的地方。 有四个要点：

  1. 时间尺度
  2. 包含组分
  3. 变量单位
  4. 假设条件

尽管无论何时(??)都是适用的，但是在不同条件下，其所具有的含义不同。例如，ΔSΔS所包含的意义。 在年尺度或多年尺度上，我们关心的储量变化是冰川体积、土壤含水量、地下水（冰）储量、湖泊储水量、河道储水量。 但在较小的时间尺度上（日、月），我们需要需要考虑植被储水量、积雪、人类活动中的取用水量等。在小时尺度上，则需要考虑地表积水、植被截留等。小时间尺度上所关心的变量在长时间尺度上往往可以忽略不计，或者因为长时间的平均效应而趋近于0。例如，积雪。在日和月尺度上，一部分降水在冬季以降雪的形式出现，在地表形成积雪，这些积雪将在几个月的夏季进入融化状态。冬季积雪储量处于增加状态，在夏季则逐渐融化释放，在下一个冬季来临之前基本全部融化。在月的尺度上看，积雪储量始终都在变化，是不可忽略的因素。而在多年尺度上，积雪在一部分时间里积累、另一部分时间里面融化，积雪总储量不会增加。如果积雪多年不融化，则其将发展为冰川的形成过程，则属于是另外一个过程。

2-22-2中的单位可以是深度单位，也可以是速率单位。比如常用的立方米、毫米、毫米/年。实际的语言表达则需要注意。 当使用毫米单位时，隐含了时间信息。 例如，一个流域30年统计表明年降雨量500毫米，蒸发量200毫米，径流量300毫米。则公式写为： ΔS(0 mm)=P(500 mm)−E(200 mm)−Q(300 mm)ΔS(0 mm)=P(500 mm)−E(200 mm)−Q(300 mm)。 公式表达了在年尺度的平均水量平衡，500，200， 300等数都是一年时间范围内的平均水量。当所有变量都乘以流域面积时，上面公式的单位则表达体积水量(立方米)，表达含义相同。 公式也可以表达为ΔS(0 mm/a)=P(500 mm/a)−E(200 mm/a)−Q(300 mm/a)ΔS(0 mm/a)=P(500 mm/a)−E(200 mm/a)−Q(300 mm/a)，则显式的表达了年尺度的统计特征。 同时，以上水量平衡也可以表达为 ΔS(0×30 mm)=P(500×30 mm)−E(200×30 mm)−Q(300×30 mm)ΔS(0×30 mm)=P(500×30 mm)−E(200×30 mm)−Q(300×30 mm) ΔS(0 mm)=P(15000 mm)−E(6000 mm)−Q(9000 mm)ΔS(0 mm)=P(15000 mm)−E(6000 mm)−Q(9000 mm) 则其表达的是30年时间范围的的总水量平衡。

2.2.2 边界条件

对于流域问题，基本的边界条件假设为： 1. 流域为封闭边界，即，（除了出口径流外），没有外部水源从水平方向补给流域，流域也不存在水平方向上向外部输出过程。 2. 降水为垂直方向的外部物质输入。 3. 流域底部存在一个零通量（不透水）的基岩面。这一假设在绝大部分条件下成立；在某些已知深层基岩或深层地下水活动的情境下，可以灵活设置透水底部边界条件。

2.3 气象驱动

2.3.1 降雨

2.3.2 蒸散发

2.3.3 风廓线 (Wind profile)

Equation 2.3 in (Abtew and Melesse 2012)

ux=umlnzx−dz0lnzm−dz0

  • ux - 目标高度的风速 [ms−1]
  • um - 测量高度的风速 [ms−1]
  • zx - 目标高度 [m]
  • zm - 测量高度 [m]
  • d - 零平面 [m]
  • z0 - 粗糙度(Roughness height) [m]

FAO56

  1. 植被覆盖的

  2. 开放水面和裸露土地的潜在蒸发(PET of bare soil and open water) λEa=c2ea−edra

Ea 是同温蒸发率(Isothermal evaporation rate)。

Eo=Δ(Rn−G)/λ+γEaΔ+γ

2.4 能量过程

** *能量过程的计算仅在陆面-水文耦合的L-SHUD模型中启用 **

2.4.1 辐射

→L=L↑−Latm↓

Trad=(L↑σ)1/4

L↑=(1−εg)Latm↓+εgσ(Tng)4+4εgσ(Tng)3(Tn+1g−Tng)

2.4.2 地表能量平衡

Rn+Lw=Hl+Hs+G

  • Rn： 短波辐射(input)
  • Lw： 长波辐射(input)
  • Hl： 潜热
  • Hs： 感热
  • G： 土壤热通量

H=−ρatmCp(θatm−θs)rah

eatm=qatmPatm0.622+0.378qatm

ρatm=Patm−0.378eatmRdaTatm

在陆面模型中，地表辐射能量平衡的计算涉及到多个物理过程和参数。以下是一些基本的计算公式：

  1. 地表反照率（Albedo, a）: a=RreflectedRincoming 其中，Rreflected 是反射的太阳辐射，Rincoming 是入射的太阳辐射。

  2. 吸收的太阳辐射（Rabsorbed）: Rabsorbed=Rincoming−Rreflected

  3. 地表发射的长波辐射（Lemitted）: Lemitted=ϵσT4 其中，ϵ 是地表的发射率，σ 是斯特藩-玻尔兹曼常数（约为 5.67×10−8 W m^-2 K^-4），T 是地表温度。

  4. 大气发射的长波辐射（Latm）: Latm=ϵatmσT4atm 其中，ϵatm 是大气的发射率，Tatm 是大气温度。

  5. 净长波辐射（Lnet）: Lnet=Lemitted−Latm

  6. 净辐射（Rnet）: Rnet=Rabsorbed−Lnet

  7. 感热通量（QH） 和 潜热通量（QE）: 这些通量通常与地表能量平衡的其他组成部分一起计算，它们与地表温度、湿度和风速有关。

  8. 土壤热通量（G）: G=导热项+对流项+辐射项 土壤热通量是土壤内部热量传递的量，通常通过数值方法求解。

  9. 能量平衡闭合: Rnet+QH+QE+G=0 这个方程确保了能量的守恒。

请注意，这些公式是简化的表示，实际的模型可能会包含更多的细节和复杂性，例如考虑不同波长的辐射、不同地表类型的反照率变化、云层的影响等。此外，模型中还可能使用经验公式或参数化方案来近似某些过程。如果你需要更详细的信息或者特定于CLM 5.0模型的公式，你可能需要查阅该模型的文档或源代码。

2.5 模型结构及原理

SHUD已广泛应用于不同水文气候和多种尺度的水文过程模拟，时间尺度从小时至百年，空间尺度从1平方米至100,000平方公里，涵盖北美洲、亚洲和非洲等多个流域的湖泊、洪水和水资源研究等（Shu et al., 2020; Gil et al., 2021; 舒乐乐 等，2022）。基于Freeze和Harlan的“基于物理的水文响应模型蓝图”（Freeze & Harlan, 1969），SHUD模型利用理查兹方程（公式2-1）计算地下水流动，利用曼宁公式（公式2-4）计算地表水流动，利用圣维南方程（公式2-2）描述计算地表水质量守恒，利用（公式2-3）描述地下水质量守恒（舒乐乐 等，2022，2024）。SHUD在前期数据准备阶段随机划分计算单元，能够精细描述研究区地形土壤及气象等要素分布特征和描述流域的水文物理过程，实现对区域乃至全局水文响应的综合模拟，源代码和详细说明书可通过项目网站（https://www.shud.xyz）或GitHub页面（https://github.com/shud-system/shud）获得。

q=−ke(h)∇(h+z)

∂h∂t=∇⋅(vh)−QeA+QsuAc

Sw(h)∂h∂t=∇⋅q+QeV+Qssv

v=n−1R23S12f

其中，

  • q为流量，单位为L3L−2T−1；
  • h为水头高度，单位为L；
  • ke(h)为水力传导度，是土壤含水量或者基质势的函数，单位为LT−1；
  • z为高程，单位为L；v为流速，单位为LT−1；t为时间，单位为T；
  • A为控制单元垂直投影面积，单位为L2；
  • Qe为地表与地下水交互流量，单位为L3T−1；
  • Qsu为地表水的源汇项，单位为L3T−1；
  • Sw(h)为储水系数，其物理含义为其物理意义为含水层的水头降低/升高一个单位时，单位体积的含水层释放/吸收的水量，单位为L3L−3L−1；
  • V为控制单元体积，单位为L3，
  • Qss为地下水或土壤水的源汇项，单位L3T−1；
  • n为曼宁系数，单位为TL−1/3；
  • R为水力半径，单位为L；
  • Sf为摩擦坡度，单位为LL−1。

SHUD是典型地表－地下耦合的数值方法分布式水文模型，其与其他模型相比所具有的优势也是本研究选择该模型进行研究最主要的原因。地表－地下全过程耦合的分布式水文模型作为分布式模型中一个特殊类别，相较于传统分布式水文模型，实现了利用数值方法将地表－地下水文过程的物理耦合，可以更好地刻画复杂地形地貌水文过程，也能更好表达流域空间异质性（舒乐乐 等，2022）。物理性分布式水文模型在表达空间异质和刻画水文过程中优于概念模型和集总式模型（舒乐乐 等，2022）。

时空连续性是数值方法模型相比于传统水文模型的显著优势。在时间离散方面，SHUD采用有限体积法求解流域水文学的常微分方程，包括地表水流、非饱和层和饱和层流动以及河道水流过程，以获得空间上的水储量和流量。空间网格可以分为非结构如不规则的三角形和结构化如正方形，SHUD模型使用非结构化三角形网格。SHUD模型保证了水文变量的连续性、一致性和收敛性，也保证了模型局地和全局的水量平衡。数值方法一个典型特征是地表和地下耦合，圣维南方程跟理查兹方程要耦合起来，SHUD模型使用一阶变量交换，主要指地表地下水的交互之间的变量交换。SHUD模型耦合方式为全局隐式，地表水储量的水头高度与地下水和土壤水水头高度在同一个方程中。河道与坡面单元关系有相邻和交叉的方式，SHUD模型使用交叉方法，优势在于网格的密度与河流的绵延程度及分割长度等河流单元的分辨率无关，使得每个单元和固定相交的某个河道单元进行水量交互。空间离散上，坡面和河流分别使用非结构性三角形网格和梯形河道单元描述，垂直方向包括地表层、非饱和层和饱和层。因为在较大尺度上，非饱和层水平流动水量远小于垂直方向流量，因此部分模型忽略壤中流计算或者实质上将其隐含在地表和地下水水平流动中（Shu et al., 2020）。

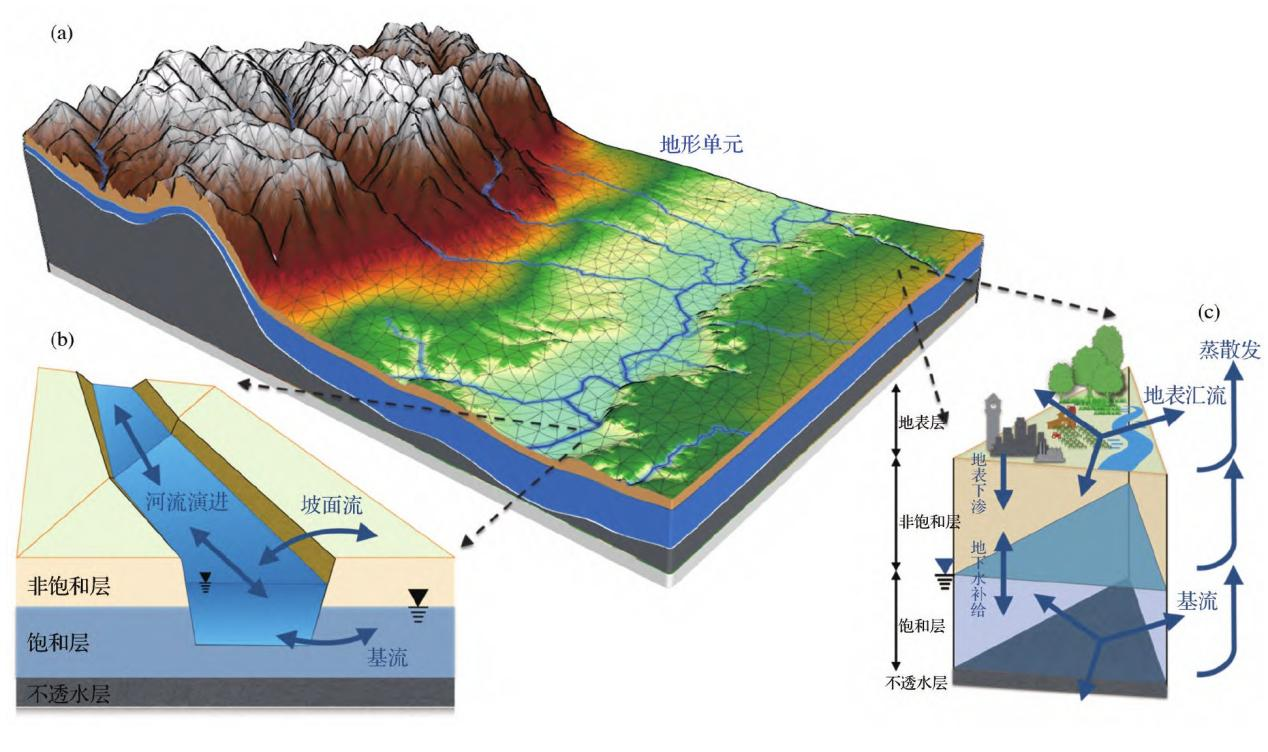
图2-4 SHUD模型的水平空间结构（a）、河流网络拓扑关系（b）和垂直分层关系（c）（引自舒乐乐 等，2022）Figure 2-4 The lateral spatial structure(a), river topology(b) and vertical layers(c)
图2-4 SHUD模型的水平空间结构（a）、河流网络拓扑关系（b）和垂直分层关系（c）（引自舒乐乐 等，2022）Figure 2-4 The lateral spatial structure(a), river topology(b) and vertical layers(c)

本文只介绍 SHUD模型的基本原理，其原理图如图2-3所示，具体细节及更新可以参考（Shu et al., 2020, 2024a,2024b）以及其后续发展的文章。模型模拟的过程包括植被截流、融雪积累/消融、蒸散发、入渗、地下水补给、地表坡面流、地下水基流和河道双向流动等。

2.5.1 植被冠层截留

植被冠层截留：指暂时保存在植物表面及枝干的部分降水，即被植被拦截的降水量。在降水初期或降水量较小时，几乎全部降水被植被截留；达到最大截留量之后，降水全部下落至地面。在SHUD模型中，将截流过程类比为水桶模型，水桶的最大蓄水量即为最大截留量。若现有截留量小于等于0，当降水小于最大截留量，则截留量等于降水；当降水大于最大截留量，则截留量为最大截留量；若现有截留量大于0但小于最大截留量，则截留量为最大截留量与现有截留量之差或当前降水中的较小值；若当前截留量大于等于最大截留量时，拦截能力为0，即此时及之后的所有降水全部穿过植被到达地表。最大截留量计算公式如下：

S∗ic=CicLAI

其中：

  • Cic为截留系数，单位为m，默认值为0.2 kgm−2（Dickinson, 1984）；
  • LAI为叶面积指数（leaf area index），单位为m2m−2；S∗ic为最大截留量，单位为m。

截留量计算公式如下：

qic=min[s∗icΔt,P]Sic≤0min[ S∗ic−Sic)Δt,P]0<Sic<S∗ic0 Sic≥S∗ic

其中：

  • Sic为现有截留量，单位为m；
  • qic为截留量，即冠层截流后保存于植物表面的部分降水，单位为md−1;
  • P为降水量，单位为md−1。

冠层截留水量平衡方程描述冠层截留水储量随时间变化的过程，即冠层水储量等于截留量减去冠层截流水的蒸发量。其中，截留量是降水量减去穿透冠层到达地表的降水量，即被植被截留的部分；冠层截流水的蒸发量是指截留在植被上的水分通过蒸发释放到大气中的过程。其公式如下：

dSicdt=qic−Eic

其中：

  • Eic为冠层截流水的蒸发量，单位为m3m−2d−1。

2.5.2 蒸散发

蒸散发：是流域水分流失的主要途径，包含陆地上通过蒸发和植被蒸腾向上流失的水分之和，是全球和流域水文循环中的重要环节。潜在蒸散发：指水量充足条件下蒸散发量，采用联合国粮农组织FAO（Food and Agriculture Organization of the United Nations）推荐使用的彭曼-蒙斯特公式PM（Penman-Monteith）计算，计算公式如下：

E0=1λΔ(Rn−G)+ρacp(es−ea)raΔ+γ(1+rsra)

其中，

  • E0为使用PM公式计算的潜在蒸散发，单位为kgm−2s−1；
  • λ为蒸散发潜热，单位为MJkg−1；
  • Δ为饱和水汽压对应温度曲线的斜率，单位为kPaK−1；
  • Rn为净辐射，单位为MJm−2s−1；G为地面热量损失，单位为MJm−2s−1；
  • ρa为空气密度，单位为kgm−3；
  • cp为空气比热容量，单位为MJkg−1K−1；
  • es为气温下的空气饱和水汽压，单位为kPa；
  • ea为气温下的空气水汽压，单位为kPa；
  • ra为总体空气动力学扩散阻抗，单位为sm−1；
  • rs为总体冠层扩散阻抗，单位为sm−1；
  • γ为湿度常数，单位为kPa。

实际蒸散发是由截留蒸发Ec、土壤直接蒸发Es和植被蒸腾Et三部分组成的水分蒸发。Ec为截留蒸发为冠层水储量对应的潜在蒸散发的最大值。计算公式如下：

Ec=max[Sic/Δt,E0]

土壤直接蒸发Es为土壤表面直接蒸发的水分量，植被蒸腾Et为指植物通过根部吸收土壤中的水分，经过植物体内的蒸腾过程释放到大气中的水分量，两者之和为地表实际蒸发。Es由积水蒸发Esp和土壤水分蒸发Esm组成。计算过程中，首先考虑积水的蒸发，当积水量满足蒸发时，只消耗地表积水；否则Es则由全部地表积水和土壤水分组成；当地表无积水时Es只由土壤水分组成。计算公式如下：

Esp=EsEsm=0ysf>Es×Δt{Esp=ysf/dtEsm=Es−Espysf<Es×ΔtEsp=0Esm=Esysf≤0

其中，ysf为地表积水，单位为m。

潜在蒸散量（PET）是使用PM公式计算的，而实际蒸散量（AET）是通过将PET乘以土壤水分胁迫系数得出的，该系数由土壤含水量和地下水位深度决定。

Es=E0βs(1−αimp)(1−αveg )

其中，

  • βs为土壤水分胁迫系数；
  • αimp为不透水面积分数；
  • aveg为植被覆盖度。

Et由来自土壤水和地下水两部分组成，当地下水位高于根深时，植被蒸腾使用地下水，蒸腾时对应的土壤水分胁迫βs为1，因为此时植物根系可以获取充足的水分，蒸腾对土壤水分的利用没有限制。

Et=E0βs(1−αimp)αveg

。土壤水分胁迫是指土壤中水分供应不足导致植物受到水分限制的状态，此时植物生长及其蒸腾都受水分多少的影响。βs是水文模型中考虑的重要参数之一，综合考虑ɑimp和βs有助于更全面展现土壤蒸发和植被蒸腾的过程，计算公式如下：

βs=θ−θrθfc−θr

其中，

  • θ为土壤含水量；
  • θfc为田间持水量；
  • θr为剩余土壤含水量。

2.5.3 积雪

积雪采用度日模型：在温带或山地气候地区，降雪积累和融化是一个重要的地表过程，也是土壤水分和补给的重要来源。融化积雪产生的水量直接补给地表水。在SHUD模型中采用度日模型（degree-day model）（Finsterwalder et al., 1887）来模拟积雪的融化过程，假设融雪量与空气温度及临界温度之差成正比，可以更精准模拟积雪融化过程及其对径流的影响。通过积温来估算积雪融化量，mf为融雪因子，单位为ms−1℃−1，T为空气温度，T0为融雪时对应的临界温度，一般按照经验取值。积雪融化速度计算公式如下：

qsn=(T−T0)×mf

其中，

  • qsn为积雪融化速度，单位为ms−1。

积雪对应的水量平衡方程可以表示降雪储量，降雪储量等于降雪量减去积雪升华和积雪融化量，计算公式如下：

dSsndt=Psn−qsn

其中，

  • Ssn为积雪储量，单位为m；
  • Psn为降雪量，单位为ms−1。

2.5.4 地表水

地表坡面流近似视为二维浅水流动，使用扩散波（曼宁公式）进行计算，计算公式如下：

Qjs=Ljn¯ysf53S120

其中，

  • Qjs为三角形沿方向j的坡面漫流，单位为m3s−1；
  • Lj为单元j边长度，单位为m；n为曼宁系数，单位为sm−1/3；
  • S0为地表坡度。

¯ysf={ysfzsf+ysf≥zjsf+yjsfyjsfzsf+ysf<zjsf+yjsf

其中， - ysf为计算坡面流的有效水头高度，由两个单元之间的坡度决定，单位为m，计算公式如下：

地表水对应的水量平衡由变化水储量由净降水量Pn、入渗量qi、地表积水蒸发量Esp、地表水流动量共同决定。对应的公式如下：

dysfdt=Pn−Esp−qi−3∑j=1QjsAc

其中，

  • ysf为单元格的地表积水高度，单位为m；
  • Pn为到达地面的净降水量，单位为ms−1
  • ；Esp为地表水面蒸发量，单位为ms−1；
  • qi为入渗量，单位为ms−1；
  • Ac为三角形坡面单元面积，单位为m2。

其中净降水量Pn为考虑降水P、植被截留Sic和积雪融化Qsn后到达地面的降水量；

Pn=P−Sic+qsc

其中入渗量由理查兹方程计算，入渗发生在表层土壤，入渗速率由积水高度和土壤湿度共同决定。计算公式如下：

qi=Kei(Θ)(1+ysDinf)

其中，

  • qi为入渗速率，向下为正方向，单位为ms−1；
  • Kei为有效渗透水力传导度，单位为ms−1；为相对饱和比；
  • Dinf为下渗发生的地表土层厚度。

ys/△t将积水、灌溉和降水结合起来，共同决定表层土壤的水力梯度。表层土壤的水力梯度可以通过单位时间内的水分量（ys）除以时间间隔（△t）来计算，水分量包括来自积水、灌溉和降水的影响。

Kei(Θ)={Kr(Θ)kx(1−αh)+αhkmΘys/Δt≥KmaxKr(Θ)(1−αh)ys/Δt<Kmax

其中，

  • Kei为有效渗透水力传导度，单位为ms−1；
  • Kr为相对水力传导度，是饱和比的函数；
  • kx为表层土的饱和水力传导度，单位为ms−1；
  • ɑh为水平大孔隙面积比；
  • km为土壤大孔隙饱和水力传导度，单位为ms−1。

Kr(Θ)=Θ12(−1+(1−Θββ−1)β−1β)2

其中，Kr为相对水力传导度，是饱和比的函数；β为van Genuchten土壤参数。

Kmax由土壤基质和大孔隙共同决定。当单位时间内的水分量（ys）除以时间间隔（Δt）小于最大入渗量（Kmax），入渗受土壤基质控制，入渗速率受土壤孔隙结构和土壤水分渗透能力的影响；而当ys/Δt大于最大入渗量（Kmax）时，表示入渗速度快于Kmax，表明土壤已饱和，水分无法迅速渗透至地下，这时入渗由土壤基质和大孔隙共同决定。大孔隙通常能够提高土壤水的渗透能力，对于加快水分的入渗速度具有重要作用。SHUD模型入渗考虑了大孔隙效应，可以在强降水条件下加快入渗速度。考虑土壤中大孔隙的影响，模型能更准确地预测和模拟土壤入渗的过程，尤其在强降水条件下，大孔隙效应的考虑对于准确模拟水文过程非常重要。

Kmax=kx(1−αh)+αhkm

其中，

  • Kmax是有效土壤水力传导度，由土壤基质和大孔隙特性共同决定的入渗能力；
  • kx为表层土的饱和水力传导度，单位为ms−1；
  • ɑh为水平大孔隙面积分数，km为土壤大孔隙饱和水力传导度，单位为ms−1。

2.5.5 2.3.5 土壤水

非饱和土壤水流动视为一维垂直流动，忽略非饱和层的水平流动，使用理查兹公式计算非饱和土壤水运动。土壤水对应的水量平衡方程描述了土壤水储量由入渗、补给和土壤蒸发蒸腾量共同决定。

sydyusdt=qi−qr−Esm

其中，

  • sy为储水系数；
  • yus为非饱和水储量；
  • qi为入渗量；
  • qr为地下水补给量
  • ；Esm为土壤蒸发蒸腾量。 土壤水分含量与田间持水量的比值是描述土壤水分状况的重要指标，通常用来控制补给速率和水文过程中的水分运动。

qr=Ker (θ−θrθfc−θr)

其中，

  • qr为地下水补给速率，向下为正方向，单位为ms−1；
  • Ker有效补给水力传导度，单位为ms−1；
  • θ为土壤含水量；
  • θfc为田间持水量；
  • θr为剩余土壤含水量。

Ker=Dus+ygwDus/kx+ygw/kv

其中，

  • Ker有效补给水力传导度，单位为ms−1；
  • Dus为非饱和层厚度，单位为m；
  • ygw为地下水位（不透水基岩之上），单位为m；
  • kx为表层土的饱和水力传导度，单位为ms−1；
  • kv为饱和层的饱和垂直水力传导度，单位为ms−1。

2.5.6 地下水

达西定律描述了地下水渗流速率与水头梯度之间的关系，而Dupuit假设则认为地下水是水平均匀流动的。结合达西定律和Dupuit假设计算饱和地下水的水平流动。水量平衡方程描述了地下水储量由地下水补给量、植被由饱和层进行的蒸腾量和地下水基流共同决定。

sydygwdt=qr−Etg−3∑i=1ojgAc

其中，

  • ygw为计算单元地下水水头（不透水基岩以上）
  • ；qr为地下水补给速率，向下为正方向，单位为ms−1；
  • Etg来自饱和层的蒸腾速率，单位为ms−1；
  • Qgj为三角形沿方向j的地下水流动，单位为m3s−1。

水平地下水通量Qjg由达西定律和Dupuit–Forchheimer假设确定。两个单元之间的梯度为[(ygw+zb)−(yjgw+z_b^j})]d−1j。沿地下水流的横截面积等于Lj×ygw。

Qjg=ˉK⋅(ygw+zb)+(yjgw+zjb)dj⋅(Lj)y−gw

其中，

  • zb为不透水基岩的高度；
  • yjgw为j方向上计算单元地下水水头；
  • zjb为j方向上不透水基岩的高度；
  • Lj为单元格边j的长度，单位为m。
  • zb为不透水基岩高程；
  • Zbj是其第j个相邻单元的基准面高程，
  • dj为两个相邻单元质心之间的距离。

考虑不同单元之间的水力传导度，可以更准确地描述地下水流动方向和速率。地下水流的有效水力传导度是两个单元上有效水平水力传导度的平均值。

¯K=(Keg+Kjcg)⋅0.5

其中，

  • Keg为有效水平水力传导度，单位为ms−1。

有效水平水力传导度（Keg）是描述地下水系统中水传导能力的重要参数，是地下水位和大孔隙特征的函数。当地下水位低于大孔隙水位时，Keg等于饱和水力传导度；当地下水位高于大孔隙水位时，考虑到土壤剖面中大孔隙的水力传导度和面积分数，有效水力传导度随地下水位的升高而增大。地下水位到达地表后，有效水力传导度达到最大值，Keg随着地下水位和土壤剖面特征的变化而变化，反映了地下水对于土壤水分运动和水文过程的不同影响。每个单元的有效水平水力传导度的计算公式如下：

kgzm>zgwKeg(Θ)={zgw−zmygw(kmαv+(1−αv)kg)+kgzm<zgw

其中，

  • zm为大孔隙距基准面的高度，单位为m；
  • zgw为地下水位的高度，单位为m；
  • αv是垂直区域大孔隙分数。

zgw=ygm+zcb

2.5.7 河道水

下游河道流量Qdn使用一维扩散波方程简化为明渠曼宁（Manning）方程来计算，基于一维流动的假设计算河道中水流的运动规律，公式如下：

Qdn=Acsˉn(AcsP)23ˉS120

其中,

  • Qdn为向下游河道的体积通量，单位为m3s−1；
  • Acs为河段的横截面积，单位为m2；为平均曼宁系数，单位为sm−1/3；
  • P为河段及其下游河段的平均湿周长；
  • ˉS0为河段及其下游河段的平均坡度。

在描述河流水文过程时，采用了三角形棱柱体元素来划分河流为多个河段，并考虑地表和地下水之间的交换以 及河段的水文过程。每个河段可以被视为一个水文单元，其水文过程可以通过质量平衡公式描述。每个河道中的质量平衡由四部分组成：与河道相交的单元产生的地表流，与单元相交的横向地下水通量，上游河道的纵向水流和流向下游河道的流量。上游通量等于多个上游河段之和。河道中的水平衡方程忽略了蒸发和降水，因为流域中的开放水域面积相对较小，且开放水域面积已包含在水文单元的计算中。河道水对应的水量平衡方程如下：

dyriv dt=1Ar(j=Nc∑j=1Qjsr+j=Nc∑j=1Qjgr+j=Nu∑j=1Qjup+Qdn)

其中，

  • Qjsr为j方向上河流和坡面计算单元之间通过坡面流的体积通量，单位为m3s−1；
  • Qjgr为河流与计算单元之间通过地下水流动的体积通量，单位为m3s−1；
  • Qjup为第j个上游河段的体积通量，单位为m3s−1；
  • Qdn为流向下游河道的体积通量，单位为m3s−1；Nc为与河道相交的三角形数量；
  • Nu为上游河道数量。

河流段和坡面单元之间的地下水交换用如下公式描述。

Qsr=LsCwbs√2g|bs|

其中，

  • Qsr为河流和坡面之间坡面流的体积通量，单位为m3s−1；
  • Ls为覆盖计算单元的河段长度，单位为m；
  • Cw为排放系数，单位为m；
  • bs为河段与坡面单元间坡面流的有效高度，单位为m；

Hriv=yriv+zrb

Hcsf=yrsf+zcs

这种地形因素对于地表水文过程和水文特征的理解至关重要，陆地表面或河岸的相对高度控制着陆地表面和河段之间的水交换方向。

Hriv −Hcsf Hriv >zbank  且 Hcsf >zbank bs={H riv −zbank Hriv >zbank  且 Hcsf <zbank Hcsf −zbank Hriv <zbank  且 Hcsf <zbank 

其中，

  • Hriv为河道水头，单位为m；
  • yriv为河道水位，单位为m；
  • zrb为河床高程，单位为m；
  • Hcsf为地表水头，单位为m；
  • ysf为计算单元地表水储量，单位为m；
  • zcs为，单位为m；
  • bs为河段与坡面单元间坡面流的有效高度，单位为m；
  • Hriv为河道水头，单位为m；
  • Hcsf为地表水头，单位为m；
  • bank为河岸或者堤防相对基准面的高程，单位为m；

Qgr=Ls bg KgrHriv−Hcgw drb

其中，

  • Qgr为河流和计算单元之间的通过地下水流动的体积通量，单位为m3s−1；
  • Ls为覆盖计算单元的河段长度，单位为m；bg为河段与坡面单元间地下水有效水头高度，单位为m；
  • Kgr为计算坡面与河道地下水交换的水力传导度，单位为ms−1；
  • Hriv为河道水头，单位为m；
  • Hcgw为计算单元地下水水头，单位为m；drb为用于计算流向河流基流的河床厚度，单位为m；

Hcgw=ygw+zcb

其中，

  • Hcgw为计算单元地下水水头，单位为m；
  • ygw为地下水位（在不透水基岩之上），单位为m；
  • zcb为基岩高程，单位为m。

bg={yriv Hcgw<zrb12(yriv+Hcgw−zrb)Hcgw>zrb

其中，

  • bg为河段与坡面单元间地下水流动有效高度，单位为m；
  • yriv为河道水位，单位为m；
  • Hcgw为计算单元地下水水头，单位为m；
  • zrb为河床高程，单位为m。

Kgr=12( Krb+Keg)

其中，

  • Kgr为计算坡面与河道地下水交换的水力传导度，单位为ms−1；
  • Krb为河床饱和水力传导度，单位为ms−1；
  • Keg为有效水平水力传导度，单位为ms−1。

SHUD模型使用有限体积法（Finite Volume，FV），采用Newton-Krylov迭代方法求解非线性方程组，具体来说通过利用牛顿迭代法求解非线性系统，并结合Krylov子空间方法来高效地逼近线性方程组的解，从而求出每次牛顿迭代的改进向量。计算过程中，基于某一时刻地表水储量、土壤水储量、地下水储量和河道水储量状态值和变化率，计算下一时刻这四个值的状态值，通过这四个时刻变化量的大小判断是否收敛以及是否进入下一时刻计算流程；随后结合上文描述的水文过程计算地表、土壤、地下和河道的储量、通量和流量（Shu et al., 2020; 舒乐乐 等，2022）。

References

Abtew, W., and A. M. Melesse. 2012. Evaporation and Evapotranspiration: Measurements and Estimations. Springer Netherlands. https://books.google.com/books?id=C84zLgEACAAJ.