Chapter 6 应用案例
6.2 大气混沌系统(Chaos System in Atmosphere)
spin-up的时间与模型的设计和模型模拟的问题有关,简单的,可以这样估算:D/v. D是初始条件偏离动态平衡的幅度,V是系统中最慢的过程的新陈代谢速率。 同样是研究水文问题,有的模型代谢速度快,预热时间就短,有的模型代谢慢就需要较长代谢时间。
举例子: 海洋模型通常需要上千年的spin-up, 地下水模型spin-up时间都是几十到几百年。水文模型中,有的只需要一两年spin-up,有的耦合地下水之后需要几十年时间,陆面过程模型通常涉及的地下水比较浅,不到一年就可以完成spin-up。
以上讲的模型都可以通过spin-up,将初始条件偏离问题解决,可以说:只要时间足够长,任何的初始条件都可以接受。这类问题属于可以新陈代谢的系统。 另外有一些系统——混沌系统,对于初始条件非常敏感,初始条件的细微差异,就会导致未来不可预测——即蝴蝶效应,细微初始条件或者过程的数值波动导致结果不具有可预测性。
Definition 6.1 洛伦兹方程(Lorenz equation)描述空气流体 运动的一个简化微分方程组.1963年,美国气象学家洛伦兹(Lorenz,E. N.)将描述大气热对流的非线 性偏微分方程组通过傅里叶展开,大胆地截断而导 出描述垂直速度、上下温差的展开系数x(t),y(t),z(t)的三维自治动力系统。
\[\begin{align} \begin{array}{l}\frac{d x}{d t}=b(y-x) \\ \frac{d y}{d t}=-x z+r x-y \\ \frac{d z}{d t}=x y-a z\end{array} \end{align}\]
利用龙格-库塔方法迭代: \[\begin{align} \begin{array}{l}x(t+\Delta t)=x(t)+f_{x}\left(x^{\prime}, y^{\prime}, z^{\prime}, t^{\prime}\right) \Delta t \\ y(t+\Delta t)=y(t)+f_{y}\left(x^{\prime}, y^{\prime}, z^{\prime}, t^{\prime}\right) \Delta t \\ z(t+\Delta t)=z(t)+f_{z}\left(x^{\prime}, y^{\prime}, z^{\prime}, t^{\prime}\right) \Delta t\end{array} \end{align}\]
rm( list = ls() )
fun.reaction <- function (x, dt, t.end, rt.col = 1:3){
f1 <- function(sigma, x){
sigma * x[2] - sigma * x[1]
}
f2 <- function(rho, x){
rho * x[1] - x[1] * x[3] - x[2]
# rho * x[1] - x[2]
}
f3 <- function(beta, x){
x[1] * x[2] - beta * x[3]
# - beta * x[3]
}
NT = t.end / dt
mat= matrix(0, NT,3)
for( i in 1:NT){
x[1] = x[1] + f1(sigma, x) * dt
x[2] = x[2] + f2(rho, x) * dt
x[3] = x[3] + f3(beta, x) * dt
mat[i, ]= x
}
ret = cbind(1:NT * dt, mat[, rt.col])
colnames(ret) = c('Time', 'x', 'y', 'z')
ret= data.frame(ret)
ret
}
sigma = 10; beta = 8/3; rho = 28
x= c(1, 1, 1) # IC
t.end = 50
dt = 0.01
x0 = c(10, 2, 1)
x1 = fun.reaction(x = x0, dt, t.end)
#' ==================================================================
#' ==================================================================
x = x1
par(mfrow=c(2,2))
plot(x$x, x$y, type = 'l')
plot(x$x, x$z, type = 'l')
plot(x$y, x$z, type = 'l')
par(mfrow=c(1,1))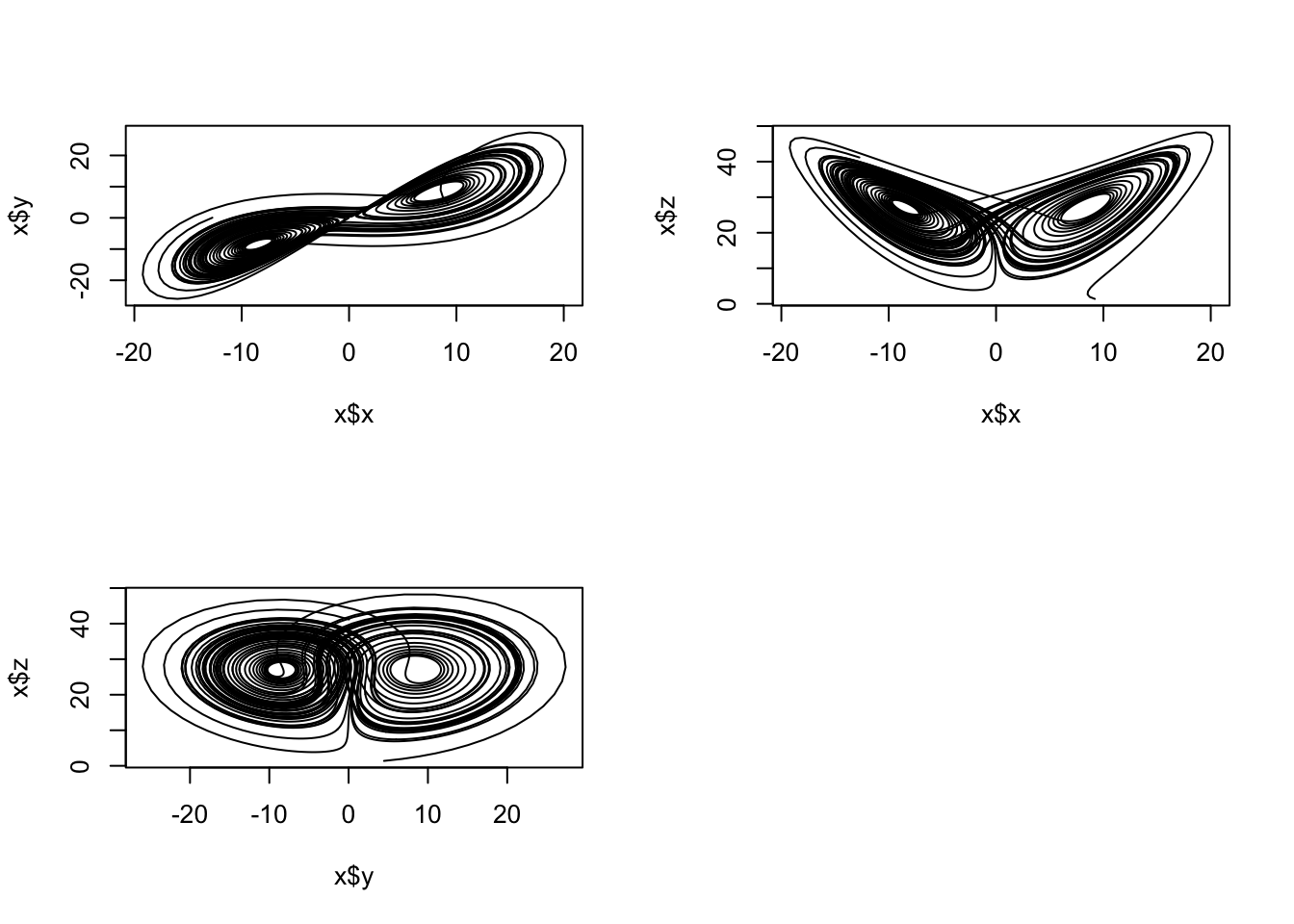
#
# rgl::plot3d(x[, 2:4])
# stop()
#' ==================================================================
#' ==================================================================
icol=1
epsilon = c(0,1,0) * 10^(-14)
x2 = fun.reaction(x = x0 + epsilon, dt, t.end)
# x2 = fun.reaction(x = x0+ c(0, 10^-13, 0), dt, t.end)
tr = (1:nrow(x1))[x1[, 1] > 40]
tr = (1:nrow(x1))[]
par(mfrow=c(3,1), mar=c(2, 4, 1, 1))
plot(x1$Time[tr], x1$x[tr], type='l', col=1, xlab='Time', ylab='X'); grid()
lines(x2$Time[tr], x2$x[tr], col=2)
plot(x1$Time[tr], x1$y[tr], type='l', col=1, xlab='Time', ylab='Y'); grid()
lines(x2$Time[tr], x2$y[tr], col=2)
plot(x1$Time[tr], x1$z[tr], type='l', col=1, xlab='Time', ylab='Z'); grid()
lines(x2$Time[tr], x2$z[tr], col=2)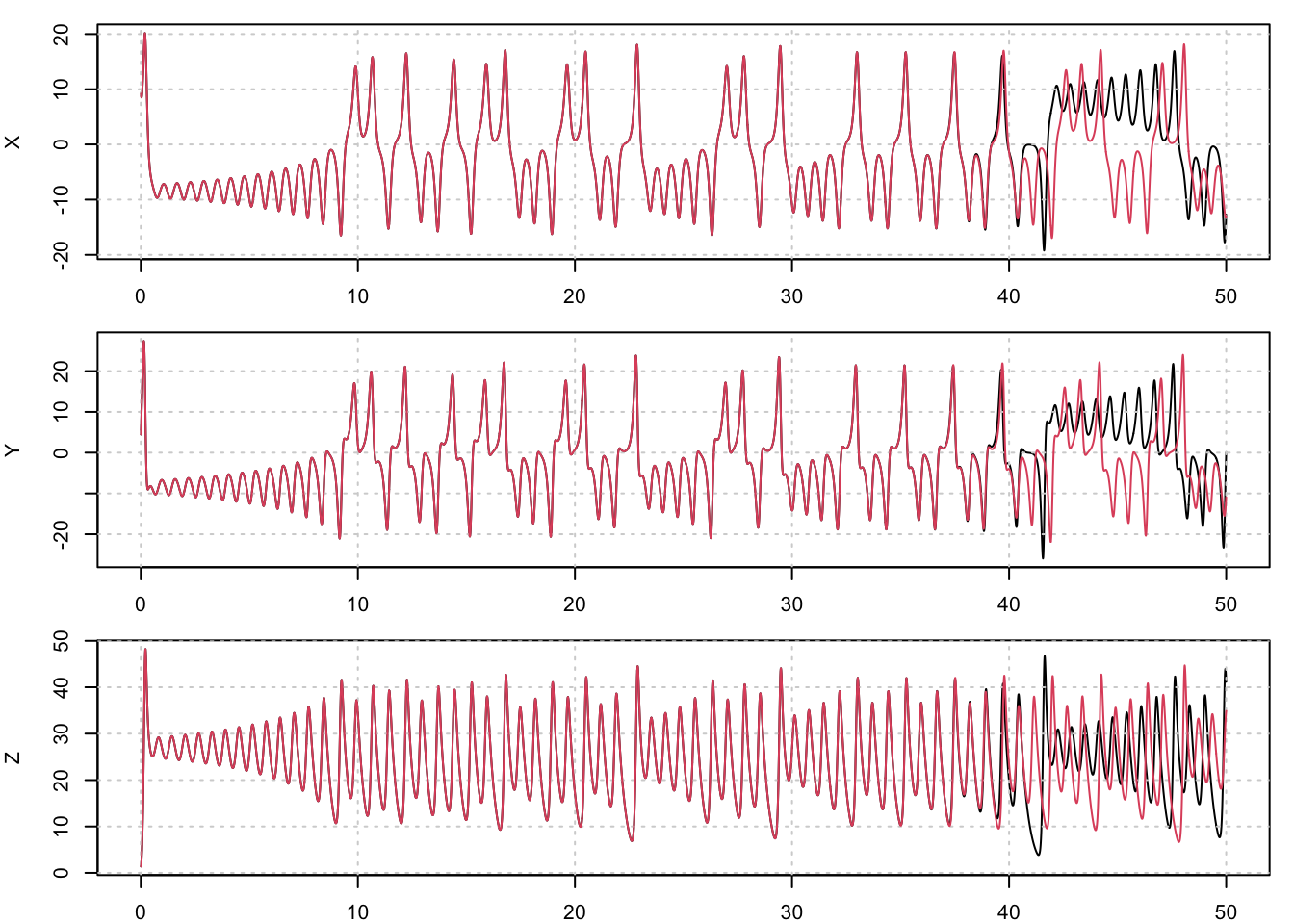
#' ==================================================================
#' ==================================================================
library(plot3D)
x=x1
par(mfrow=c(1,1), mar=c(1, 1, 1, 1))
scatter3D (x=x$x, y=x$y, z=x$z, type = "l", theta=45, phi=10, bty='b2')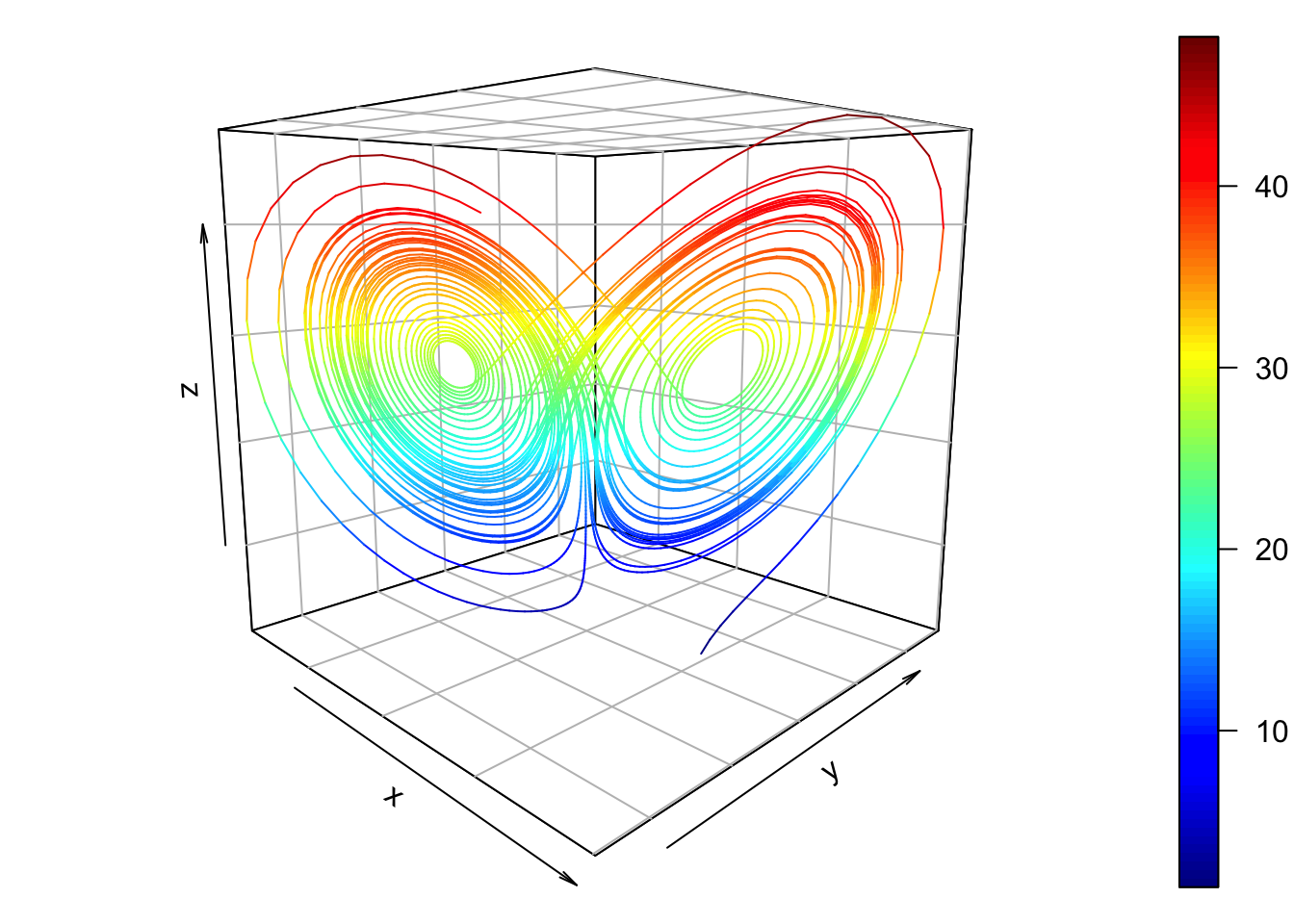
图上画的是最简单的Lorenz系统,混沌系统的代表,只有x,y,z三个变量。黑线是控制实验,红线是控制实验基础上给Y加入10的n次方波动。这张图是给Y一个\(10^{-14}\)次方的波动,结果是在40天以后,预测结果失去相关性。
6.3 承压地下水(Confined Aquifer)
6.3.1 控制方程
\[ \tag{1} s \frac{dh}{dt} = kB * \frac{d^2 h}{d x^2} + s_s \]
公式中变量含义为:
- \(s\) - 储水率 [\(L \cdot L^{-1}\)]
- \(h\) - 水头高度 [\(L\)]
- \(t\) - 时间 [\(T\)]
- \(k\) - 饱和水力传导度[\(L^3 T ^{-1} L^{-2}\)]
- \(B\) - 承压含水层厚度 [\(L\)]
- \(x\) - 沿\(x\)方向的距离 [\(L\)]
- \(s_s\) - 源汇项,即系统获得或者失去水分 [\(L T^{-1}\)]
\[\begin{equation} \begin{bmatrix} ~\beta~ & \alpha & 0 & 0 & \dots & 0 & 0 & 0 & 0\\ \alpha & ~\beta~ & \alpha & 0 & \dots & 0 & 0 & 0 & 0\\ 0 & \alpha & ~\beta~ ~& \alpha & \dots & 0 & 0 & 0 & 0\\ \dots &\dots &\dots &\dots &\dots &\dots &\dots &\dots &\dots \\ 0 & 0 & \dots & \alpha & ~\beta~& \alpha & \dots & 0 & 0\\ \dots &\dots &\dots &\dots &\dots &\dots &\dots &\dots &\dots \\ 0 & 0& 0 & 0 & \dots & \alpha~& ~\beta~ & \alpha & 0 \\ 0 & 0& 0 & 0 & \dots & 0 & \alpha & ~\beta~ & \alpha \\ 0 & 0& 0 & 0 & \dots & 0 & 0& \alpha &~\beta~ \end{bmatrix} \begin{bmatrix} h_{1}^{t} \\ h_{2}^{t} \\ h_{3}^{t} \\ h_{4}^{t} \\ \dots \\ h_{i}^{t} \\ \dots \\ h_{n-3}^{t} \\ h_{n-2}^{t} \\ h_{n-1}^{t} \\ h_{n}^{t} \end{bmatrix} = -\begin{bmatrix} h_{1}^{t-1} \\ h_{2}^{t-1} \\ h_{3}^{t-1} \\ h_{4}^{t-1} \\ \dots \\ h_{i}^{t-1} \\ \dots \\ h_{n-3}^{t-1} \\ h_{n-2}^{t-1} \\ h_{n-1}^{t-1} \\ h_{n}^{t-1} \end{bmatrix} \end{equation}\]