Chapter 3 有限差分法

3.1 泰勒展开式(Taylor Series)

在数学中，泰勒级数（英語：Taylor series）用无限项连加式——级数来表示一个函数，这些相加的项由函数在某一点的导数求得。泰勒级数是以于1715年发表了泰勒公式的英國数学家布魯克·泰勒（Sir Brook Taylor）来命名的。

泰勒展开式的基本形式：

f(x)=n∑k=0f(n)(0)n!(x)n

Taylor Series

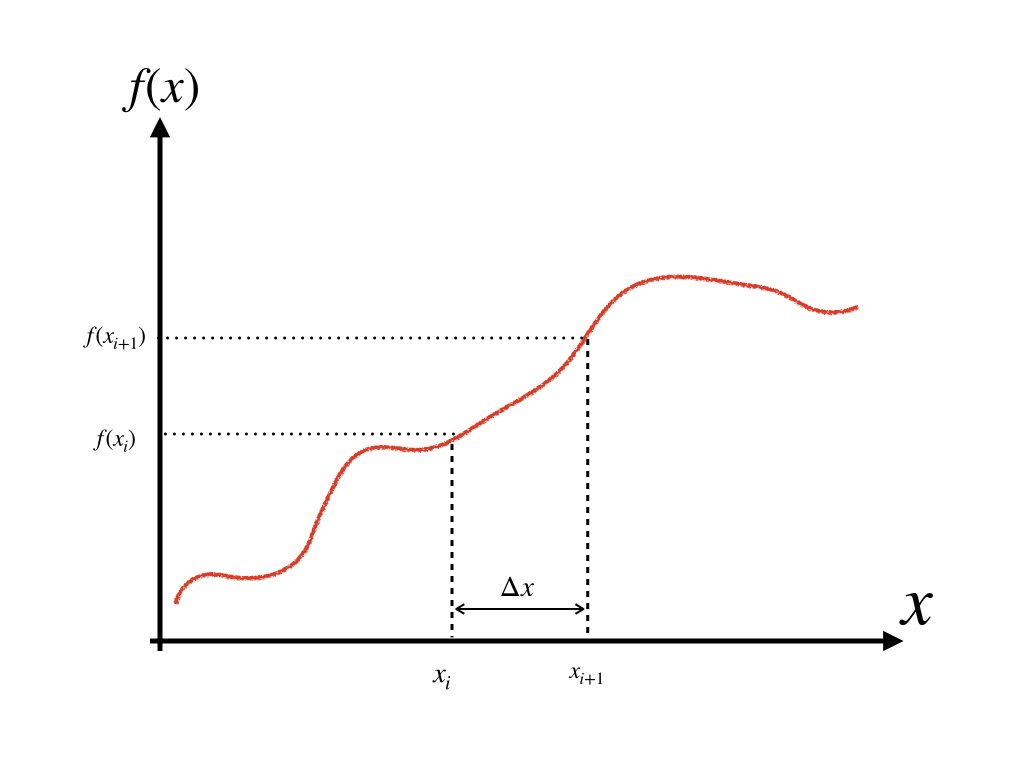
根据泰勒展开式，通过f(x)和其任意阶的导数，可以获得任意Δx值下的函数值f(x+Δx) ，即:

f(x+Δx)=f(x)+f′(x)1!Δx+f″(x)2!Δx2+f‴(x)3!Δx3+⋯+f(n)(x)n!(Δx)n

或者在−Δx位置，可写为：

f(x−Δx)=f(x)−f′(x)1!Δx+f″(x)2!Δx2−f‴(x)3!Δx3+⋯+f(n)(x)n!(−Δx)n

以上公式也可以写为： ui+1=ui+u′i1!Δx+u″i2!Δx2+u‴i3!Δx3+⋯+u(n)in!(Δx)n

ui−1=ui−u′i1!Δx+u″i2!Δx2−u‴i3!Δx3+⋯+u(n)in!(−Δx)n

在此，我们需要引入截断误差（truncation error）的概念，数学表达为O()。 O(2)和O(3)分别表示为在泰勒展开式上的二阶和三阶导数上的误差。截取误差的阶数越高，误差越小。

O(1)=u″i2!Δx2+u‴i3!Δx3+u(4)i4!Δx4+⋯+u(n)in!(Δx)n

O(2)=u‴i3!Δx3+⋯+u(n)in!(Δx)n O(3)=u(4)i4!Δx4+⋯+u(n)in!(Δx)n

何种情况下，泰勒展开式的截断误差为0？

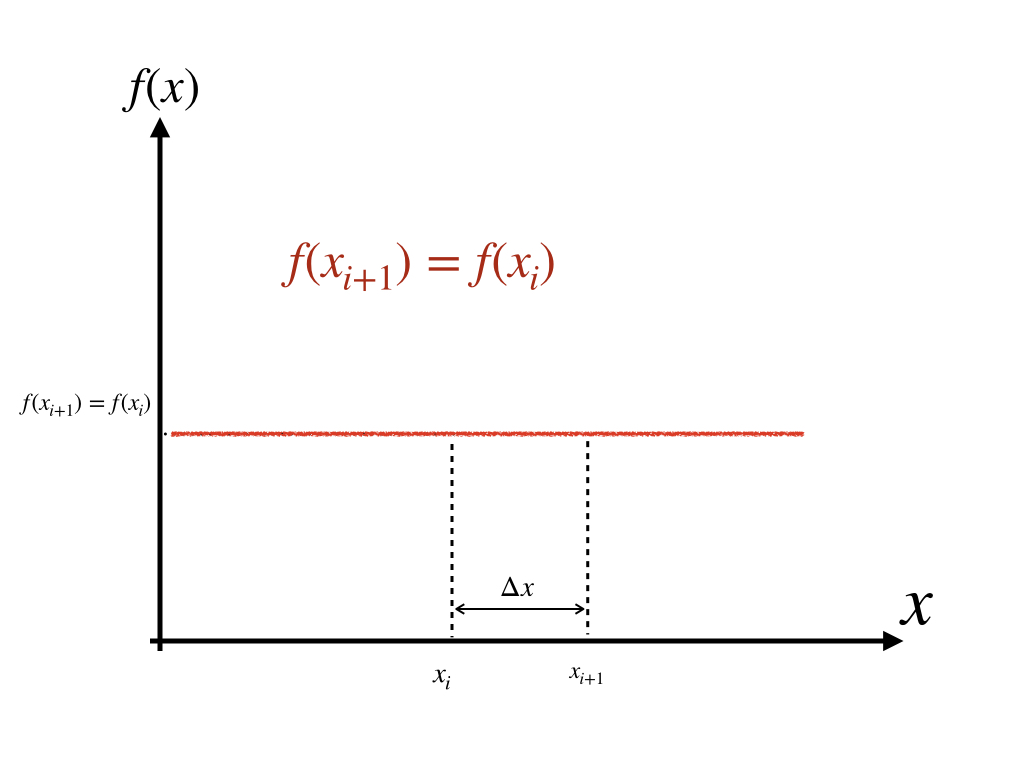
• O(0)=0 时，意味着：f(x+Δx)=f(x)。则该函数为f(x)=C, C为常数。 如图：

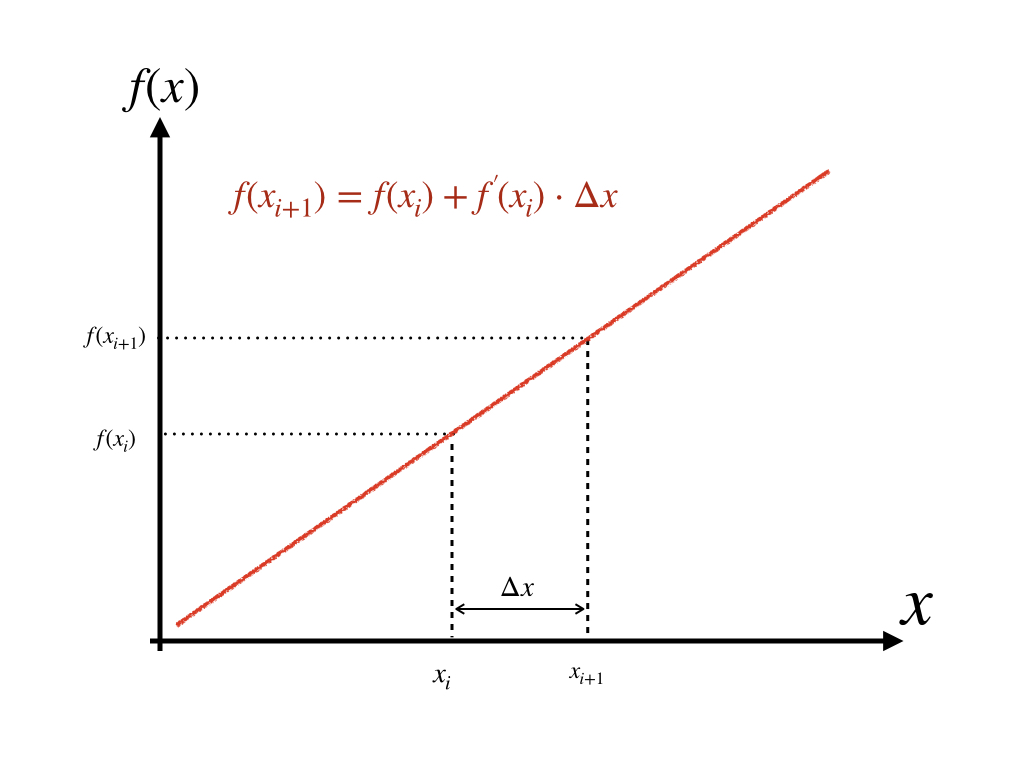
• O(1)=0 时，意味着：f(x+Δx)=f(x)+f′(x)⋅Δx。则该函数为f(x)=ax+b。 如图：

如何依据泰勒级数，得到函数的一阶和二阶导数？

3.1.1 一阶导数

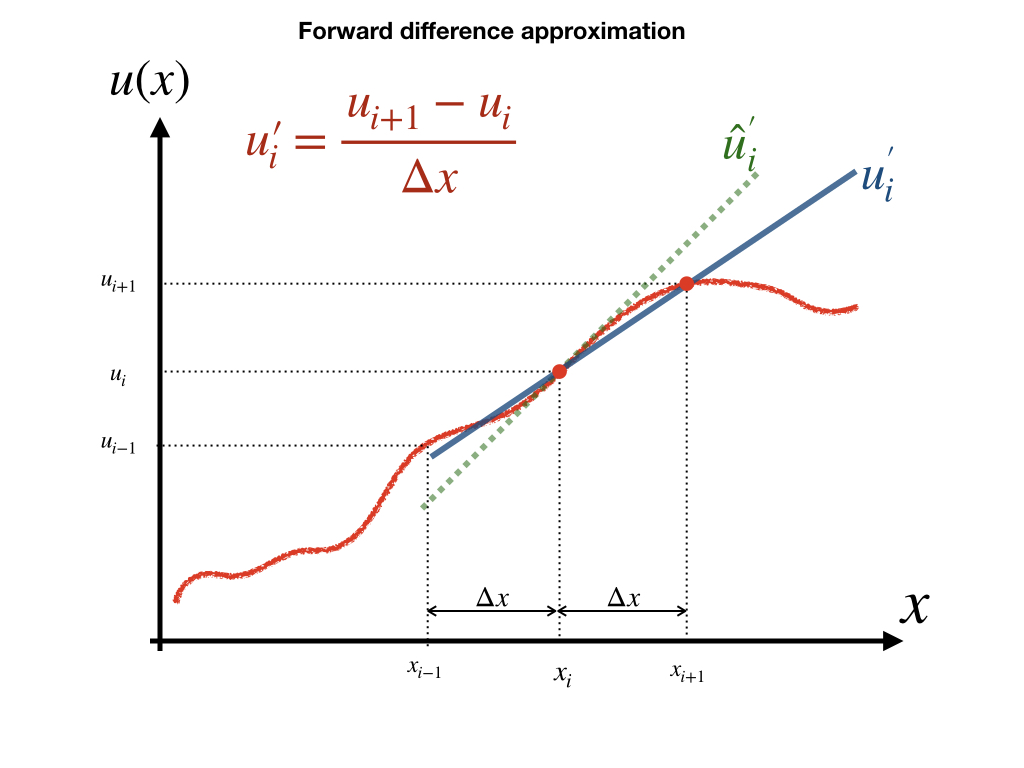
3.1.1.1 向前估计 (Forward Approximation)

采纳一阶截断误差，我们可将公式(3.2)写为： f(x+Δx)=f(x)+f′(x)1!Δx+O(1) 则： f′(x)=f(x+Δx)−f(x)Δx 或者 u′i=ui+1−uiΔx

注：公式(3.6)隐含了O(1)的误差。

向前估计

3.1.1.2 向后估计 (Backward Approximation)

采纳一阶截断误差，我们可将公式(3.3)写为： f(x−Δx)=f(x)−f′(x)1!Δx+O(1) 则： f′(x)=f(x)−f(x−Δx)Δx 或者 u′i=ui−ui−1Δx

注：公式(3.7)隐含了O(1)的误差。

向后估计

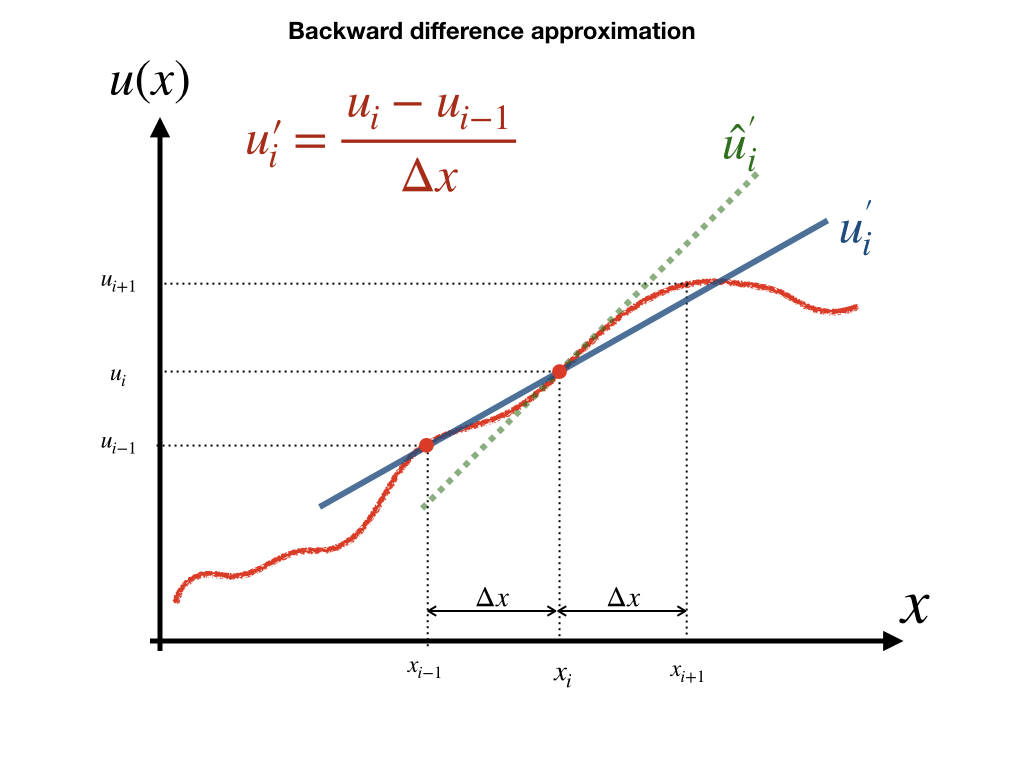
3.1.1.3 中心估计 (Central Approximation)

中心估计算法中，我们将从公式(3.2)减去公式(3.3)，得到： f(x+Δx)−f(x−Δx)=0+2∗f′(x)1!Δx+0+2∗f‴(x)3!+...

截断误差由以上公式右边的第四项（三阶导数）开始，则该公式的截取误差为O(2)，即二阶精度的截取误差，公式表达为： f(x+Δx)−f(x−Δx)=0+2∗f′(x)1!Δx+0+O(2) 可得到二阶精度的一阶导数的中心估计： f′(x)=f(x+Δx)−f(x−Δx)2Δx 或者 u′i=ui+1−ui−12Δx

公式(3.8)隐含了O(2)的误差，同时(3.6)和(3.7)都隐含了O(1)的误差。

中心估计

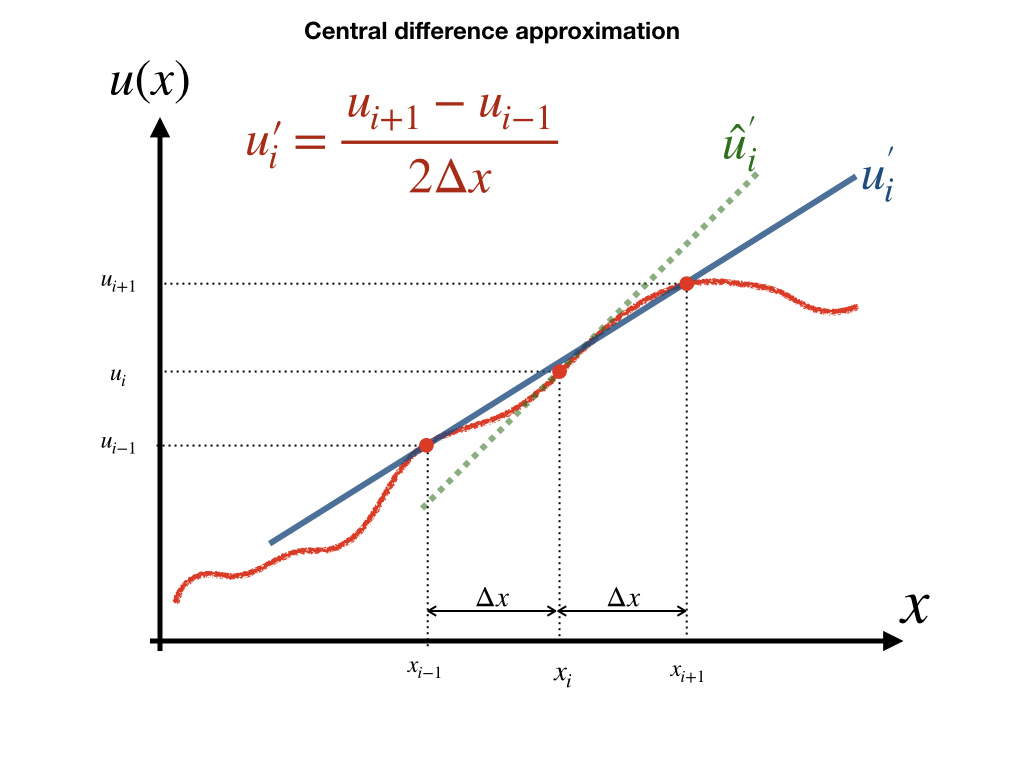
3.1.2 二阶导数

我们将公式 (3.2)和(3.3)相加，可得到：

f(x+Δx)+f(x−Δx)=2⋅f(x)+0+2⋅f″(x)2!Δx2+0+2⋅f(4)(x)4!Δx4+⋯

公式(3.9)来自公式 (3.2)和(3.3)的相加，三阶导数项在相加过程中为零，因此我们截取其三阶截取误差，则公式(3.9)可写为： f(x+Δx)+f(x−Δx)=2f(x)+f″(x)Δx2+O(3)

根据公式(3.10)，我们可获得函数f(x)在x位置的二阶导数为：

f″(x)=f(x+Δx)−2f(x)+f(x−Δx)Δx2+O(3)

当移除其三阶截断误差O(3)后，我们得到近似的二阶导数：

f″(x)≈1Δx(f(x+Δx)−f(x)Δx+f(x)−f(x−Δx)Δx)≈f(x+Δx)−2f(x)+f(x−Δx)Δx2

将公式一般化，我们可写为以下形式：

u″i≈1Δx(ui+1−uiΔx−ui−ui−1Δx)≈ui+1−2ui+ui−1Δx2

二阶导数估计

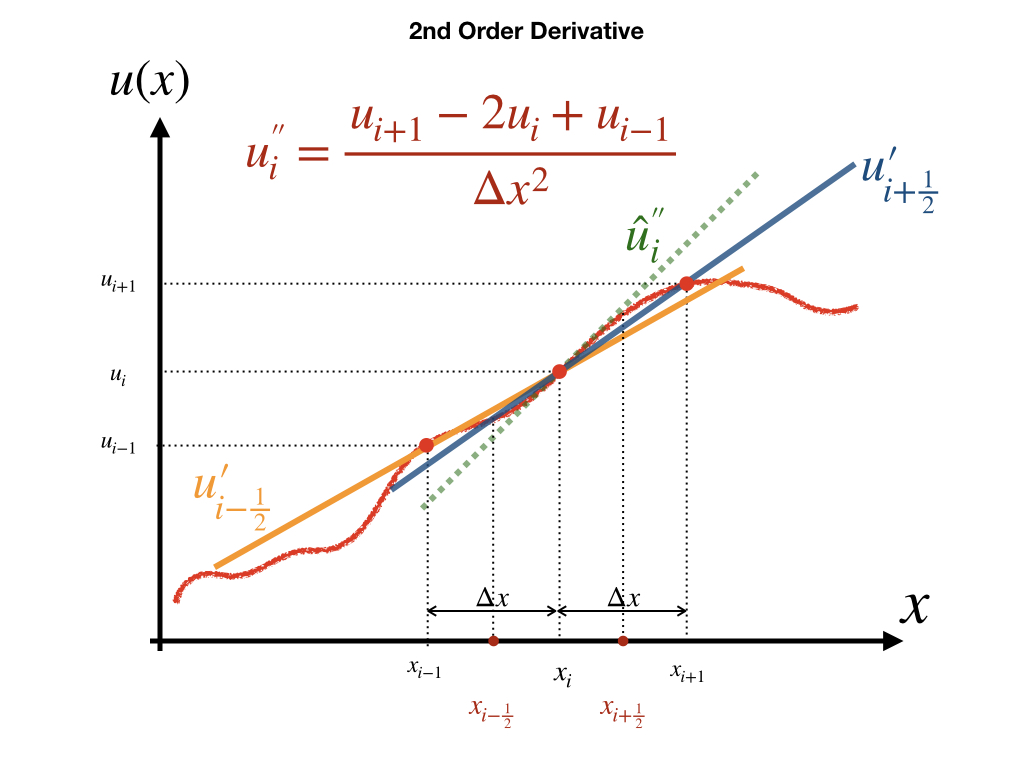
3.2 构建数值方法

Example 3.1 一根100cm长的铁棍，初始温度25 ∘C，在其左右两边分别持续施加100∘C和50∘C的温度。 求解：任意时刻铁棍的温度分布。

参考信息：

• wiki:Thermal_diffusivity
• wiki:Heat_equation

1. 问题描述

   空间微分，如图。

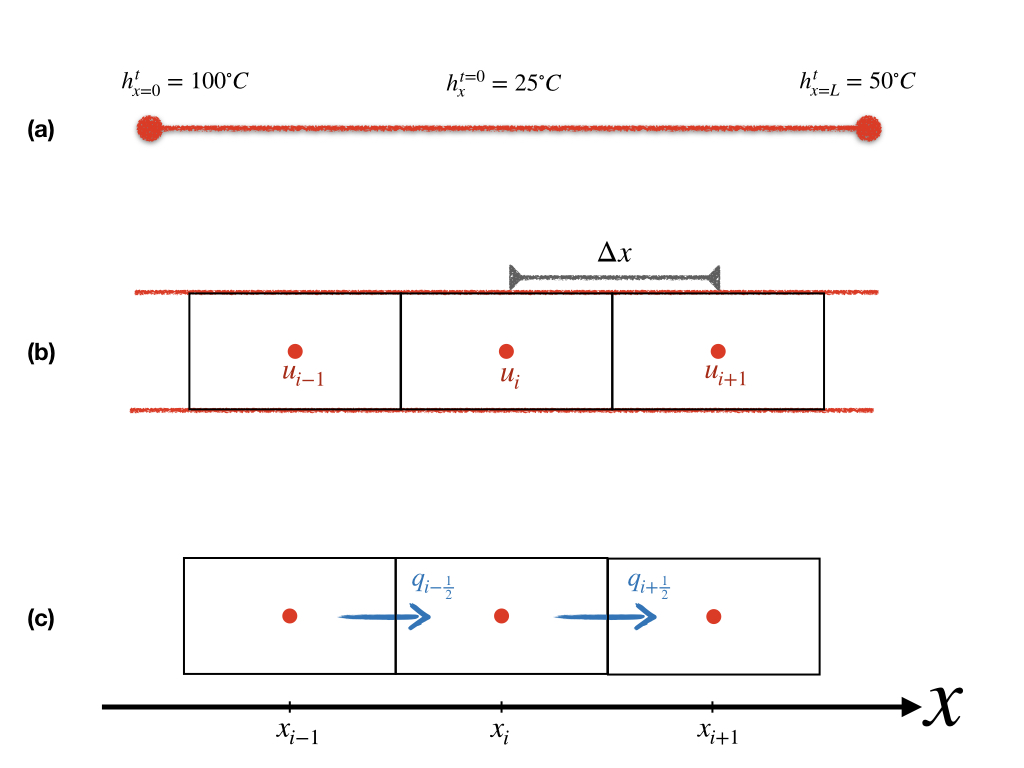
2. 物理定理

   能量守恒：
   能量变化 = 能量流入 - 能量流出 ΔE=Qin−Qout

3. 控制方程

   通量=量单位时间⋅单位面积

   • k - 热传导率[Wm−1K−1]。
   • c - 比热容(specific heat capacity)[Jkg−1K−1]。
   • ρ - 密度[kgm−3]。
   • A - 截面积[m2]。
   • D - 热力学扩散度（Thermal diffusivity）D=kρc [m2s−1]。

   ρ∗c∗Δx∗A∗Δu=qin∗A∗Δt−qout∗A∗Δt 两边同时除以ρcΔxA，得到 ΔuΔt=1ρcqin−qoutΔx 以上公式当Δx趋近与0，Δt趋近于0时，得到微分形式： ∂u∂t=1ρc∂q∂x

   q=k∂u∂x 则得到其控制方程： ∂u∂t=1ρc∂q∂x=1ρck∂u∂x∂x=D∂∂x(∂u∂x)

   令D=kρc，单位[$ m s^{-2}$]，则最终控制方程写为

   ∂u∂t=D∂2u∂x2

4. 时空离散化

   由一阶泰勒级数可知，控制方程(3.13)左边可写为： ∂u∂t=Duti−ut−1iΔt+O(1) 控制方程(3.13)左边可写为： ∂2u∂x2=ut−1i+1−2ut−1i+ut−1i−1Δx+O(3) 或者 ∂2u∂x2=uti+1−2uti+uti−1Δx+O(3)

   此时，方程左边在时间尺度上具有一阶截取误差O(1)，方程右边在空间尺度上具有三阶截断误差O(3)。省去误差项，离散化后控制方程写为： uti−ut−1iΔt=Dut−1i+1−2ut−1i+ut−1i−1Δx2 或者 uti−ut−1iΔt=Duti+1−2uti+uti−1Δx2

5. 求解

3.3 显式求解法

显式求解法以公式(3.14)作为起点，该公式可变形为： uti−ut−1i=DΔtΔx2(ut−1i+1−2ut−1i+ut−1i−1) 令α=DΔtΔx2, β=1−2α，整理以上公式可得：

uti−ut−1i=α(ut−1i+1−2ut−1i+ut−1i−1)uti=αut−1i+1+(1−2α)ut−1i+αut−1i−1uti=αut−1i+1+βut−1i+αut−1i−1

将以上公式应用于离散点上，

点号 i	公式
1	边界条件: ut1=U0
2	ut2=αut−13+βut−12+αut−11
3	ut3=αut−14+βut−13+αut−12
4	ut4=αut−15+βut−14+αut−13
5	ut5=αut−16+βut−15+αut−14
…	…
i-1	…
i	uti=αut−1i+1+βut−1i+αut−1i−1
i+1	…
…	…
n-2	utn−2=αut−1n−1+βut−1n−2+αut−1n−3
n-1	utn−1=αut−1n+βut−1n−1+αut−1n−2
n	边界条件: utn=UL

由此我们得到n个算式，可转换为矩阵形式：

[ut1ut2ut3ut4…uti…utn−3utn−2utn−1utn]=[1000…0000α β α0…00000α β  α…0000………………………00…α β α…00………………………0000…α  β α00000…0α β α0000…0001][U0ut−12ut−13ut−14…ut−1i…ut−1n−3ut−1n−2ut−1n−1UL]

更简洁的方式，可写为：

[u1u2u3u4…ui…un−3un−2un−1un]t=[1000…0000α β α0…00000α β  α…0000………………………00…α β α…00………………………0000…α  β α00000…0α β α0000…0001][U0u2u3u4…ui…un−3un−2un−1UL]t−1

下一时刻(t)的变量组成的向量x由一个矩阵[A]乘以已知的前一时刻(t−1)的向量b获得，即：。 x=[A]∗b 由已知变量的矩阵求解未知变量的方法，称为显式求解法。

3.4 隐式求解法

显式求解法以公式(3.15)作为起点，该公式可变形为： uti−ut−1i=DΔtΔx2(uti+1−2uti+uti−1) 令α=DΔtΔx2, β=−1−2α，整理以上公式可得：

uti−ut−1i=α(uti+1−2uti+uti−1)−ut−1i=αuti+1+(−1−2α)uti+αuti−1−ut−1i=αuti+1+βuti+αuti−1

将以上公式应用于离散点上，

点号 i	公式
1	边界条件: ut−11=U0
2	−ut−12=αut3+βut2+αut1
3	−ut−13=αut4+βut3+αut2
4	−ut−14=αut5+βut4+αut3
5	−ut−15=αut6+βut5+αut4
…	…
i-1	…
i	−ut−1i=αuti+1+βuti+αuti−1
i+1	…
…	…
n-2	−ut−1n−2=αutn−1+βutn−2+αutn−3
n-1	−ut−1n−1=αutn+βutn−1+αutn−2
n	边界条件: ut−1n=UL

由此我们得到n个算式，可转换为矩阵形式：

[1000…0000α β α0…00000α β  α…0000………………………00…α β α…00………………………0000…α  β α00000…0α β α0000…0001][U0ut2ut3ut4…uti…utn−3utn−2utn−1UL]=−[ut−11ut−12ut−13ut−14…ut−1i…ut−1n−3ut−1n−2ut−1n−1ut−1n]

更简洁的方式，可写为：

[1000…0000α β α0…00000α β  α…0000………………………00…α β α…00………………………0000…α  β α00000…0α β α0000…0001][U0u2u3u4…ui…un−3un−2un−1UL]t=−[u1u2u3u4…ui…un−3un−2un−1un]t−1

一个矩阵[A]乘以下一时刻(t)的变量组成的向量x等于已知的前一时刻(t−1)的向量b，求解该方程则可得到x的值，数学表达为：

[A]∗x=b

通用的求解法为 x=[A]−1∗b

通过已知变量、未知变量和矩阵组成的公式或函数来求解未知变量的过程，称为隐式求解法。

3.5 编程求解

显式求解法

#' Problem: 1D Heat Transfer
#'  governing Eqn: du/dt = k/r/c * (dd u / d x^2)
#'  wiki: https://en.wikipedia.org/wiki/Thermal_diffusivity
#'  wiki: https://en.wikipedia.org/wiki/Heat_equation
#' BC U0 = 100, UL=50
#' IC uic = 25 
#'  X = c(0, 1)
#'  D = 23 mm2/s = 2.3e-5 m^2/s
#'  DX = 0.01 m
#'  DT = 10 s
#'  Time = 0 to 1e6 s

HT.explicit <- function(
  U0=100, UL=50, uic = 25,
  X = 1,
  DX= 0.1,
  DT = 1,
  DD = 2.3e-5,
  Tmax = 1e5,
  epsilon = 1e-4, bc2 = NULL,  ignore.cfl = FALSE, plot = TRUE
){
  T0 = 0
  tt = seq(T0, Tmax, DT)
  NT = length(tt)
  xx = seq(0, X, DX)
  NX = X / DX + 1
  
  alpha = DD  * DT / (DX * DX)
  beta = 1-2*alpha
  CFL = DD  * DT / (DX * DX)
  print(CFL)  
  if(!ignore.cfl){
    if(CFL >=1 ){
      stop()
    }
  }
  #' =========================================
  x0 = rep(uic, NX)
  #' =========================================
  ylim = c(min(x0), max(U0, UL))
  xlim=c(0, X)
  if(plot){
    plot(xx, x0, type='b', col=2,  lwd=3, ylim=ylim, xlim=xlim, xlab=xlab, ylab=ylab)
    grid()
    lines(x=c(1,1) * 0, y=c(min(x0), U0), lwd=2, col=3, type='b')
    lines(x=c(1,1) * X, y=c(min(x0), UL), lwd=2, col=3, type='b')
    text(x=X/2 , y = uic + diff(ylim)*.051, 'Initial condition', font=2)
    text(x=X * 0.05 , y = U0, 'BC 1', font=2)
    text(x=X * 0.95 , y = UL, 'BC 2', font=2)
  }
  #' =========================================
  mat = matrix(0, nrow = NX, ncol = NX)
  for(i in 1:NX){
    for(j in 1:NX){
      if(i==j){
        mat[i, j] = beta
      }
      if(i+1 == j | i-1 == j ){
        mat[i, j] = alpha
      }
    }
  }
  mat[1,]=c(1, rep(0, NX-1))
  mat[NX,]=c(rep(0, NX-1), 1)
  
  xm = matrix(NA, nrow=NX, ncol=NT)
  vs = cbind(rep(0, NX))
  # vs[NX/2] = ss
  
  b=bx = cbind(x0)
  for(i in 1:NT){
    if(i>1){
      bx = mat %*% b + vs * DT
      if(any(is.nan(bx))) { break }
      if(mean(abs(b-bx)) < epsilon) { break }
    }
    bx[1] = U0
    bx[NX] = UL
    xm[, i]=bx
    b = bx
  }
  NT = i
  xm=xm[, 1:NT]
  # message('CFL value = ', CFL)  
  # message('Total Timesteps (dt * nt)= ', DT, ' * ', NT)
  yy = xm; yy[abs(yy)>1e20] = NA
  ret = list('x' = xx, 
             'time' = tt,
             'u' = xm,
             'CFL' = CFL,
             'DT' = DT,
             'NT' = NT,
             'xlim' = xlim,
             'ylim' = ylim)
  return(ret)
}
plot1 <- function(x, nout = 20){
  NT = x$NT
  id=10^seq(0, log10(x$NT), length.out = nout)
  col=colorspace::diverge_hcl(n=length(id)); lty=1
  matplot(x=x$x, y=x$u[, id], type='l', ylim=x$ylim, xlim=x$xlim, 
          xlab=xlab, ylab=ylab, col=col, lty=lty)
  legend('topright', paste0('T=', x$time[id]+1), col=col, lty=lty, bg='transparent')
  mtext(text = paste('CFL =', x$CFL ), side=3, cex=1.5)
}
plot2 <- function(x){
  NT = x$NT
  id = c(2, 4, 6, 8); nid=length(id)
  lty=1:nid; col=lty
  matplot(t(x$u[id, ]), type='l', xlab=xlab, ylab=ylab, col=col, lty=lty); grid()
  legend('bottomright',col=col, lty=lty, paste('Node', id))
}

隐式求解法

#' Problem: 1D Heat Transfer
#'  governing Eqn: du/dt = k/r/c * (dd u / d x^2)
#'  wiki: https://en.wikipedia.org/wiki/Thermal_diffusivity
#'  wiki: https://en.wikipedia.org/wiki/Heat_equation
#' BC U0 = 100, UL=50
#' IC uic = 25 
#'  X = c(0, 1)
#'  D = 23 mm2/s = 2.3e-5 m^2/s
#'  DX = 0.01 m
#'  DT = 10 s
#'  Time = 0 to 1e6 s

HT.implicit <- function(
  U0=100, UL=50, uic = 25,
  X = 1,
  DX= 0.1,
  DT = 1,
  DD = 2.3e-5,
  Tmax = 1e5,
  epsilon = 1e-4, bc2 = NULL,  ignore.cfl = FALSE, plot = TRUE
){
  T0 = 0
  tt = seq(T0, Tmax, DT)
  NT = length(tt)
  xx = seq(0, X, DX)
  NX = X / DX + 1
  
  alpha = -DD  * DT / (DX * DX)
  beta = 1 + 2 * DD  * DT / (DX * DX)
  CFL = DD  * DT / (DX * DX)
  print(CFL)  
  if(!ignore.cfl){
    if(CFL >=1 ){
      stop()
    }
  }
  #' =========================================
  x0 = rep(uic, NX)
  #' =========================================
  ylim = c(min(x0), max(U0, UL))
  xlim=c(0, X)
  if(plot){
    plot(xx, x0, type='b', col=2,  lwd=3, ylim=ylim, xlim=xlim, xlab=xlab, ylab=ylab)
    grid()
    lines(x=c(1,1) * 0, y=c(min(x0), U0), lwd=2, col=3, type='b')
    lines(x=c(1,1) * X, y=c(min(x0), UL), lwd=2, col=3, type='b')
    text(x=X/2 , y = uic + diff(ylim)*.051, 'Initial condition', font=2)
    text(x=X * 0.05 , y = U0, 'BC 1', font=2)
    text(x=X * 0.95 , y = UL, 'BC 2', font=2)
  }
  #' =========================================
  mat = matrix(0, nrow = NX, ncol = NX)
  for(i in 1:NX){
    for(j in 1:NX){
      if(i==j){
        mat[i, j] = beta
      }
      if(i+1 == j | i-1 == j ){
        mat[i, j] = alpha
      }
    }
  }
  mat[1,]=c(1, rep(0, NX-1))
  mat[NX,]=c(rep(0, NX-1), 1)
  
  xm = matrix(NA, nrow=NX, ncol=NT)
  vs = cbind(rep(0, NX))
  # vs[NX/2] = ss
  b=bx=cbind(x0)
  for(i in 1:NT){
    if(i>1){
      bx = solve(mat, b)
      if(any(is.nan(bx))) { break }
      if(mean(abs(b-bx)) < epsilon) { break }
    }
    bx[1] = U0
    bx[NX] = UL
    xm[, i]=bx
    b = bx
  }
  NT = i
  xm=xm[, 1:NT]
  # message('CFL value = ', CFL)  
  # message('Total Timesteps (dt * nt)= ', DT, ' * ', NT)
  yy = xm; yy[abs(yy)>1e20] = NA
  ret = list('x' = xx, 
             'time' = tt,
             'u' = xm,
             'CFL' = CFL,
             'DT' = DT,
             'NT' = NT,
             'xlim' = xlim,
             'ylim' = ylim)
  return(ret)
}
plot1 <- function(x, nout = 20){
  NT = x$NT
  id=10^seq(0, log10(x$NT), length.out = nout)
  col=colorspace::diverge_hcl(n=length(id)); lty=1
  matplot(x=x$x, y=x$u[, id], type='l', ylim=x$ylim, xlim=x$xlim, 
          xlab=xlab, ylab=ylab, col=col, lty=lty)
  legend('topright', paste0('T=', x$time[id]+1), col=col, lty=lty, bg='transparent')
  mtext(text = paste('CFL =', x$CFL ), side=3, cex=1.5)
}
plot2 <- function(x){
  NT = x$NT
  id = c(2, 4, 6, 8); nid=length(id)
  lty=1:nid; col=lty
  matplot(t(x$u[id, ]), type='l', xlab=xlab, ylab=ylab, col=col, lty=lty); grid()
  legend('bottomright',col=col, lty=lty, paste('Node', id))
}

3.6 显式与隐式求解法对比

3.6.1 CFL条件

source("Code/ch03/ch3_HeatTransferIm.R")
xlab ='Distance (m)'
ylab = 'Temperature (C)'
x = HT.implicit(DX= 0.05, DT = 1000, U0=100, UL=50, uic = 25, ignore.cfl=TRUE, plot=FALSE)

## [1] 9.2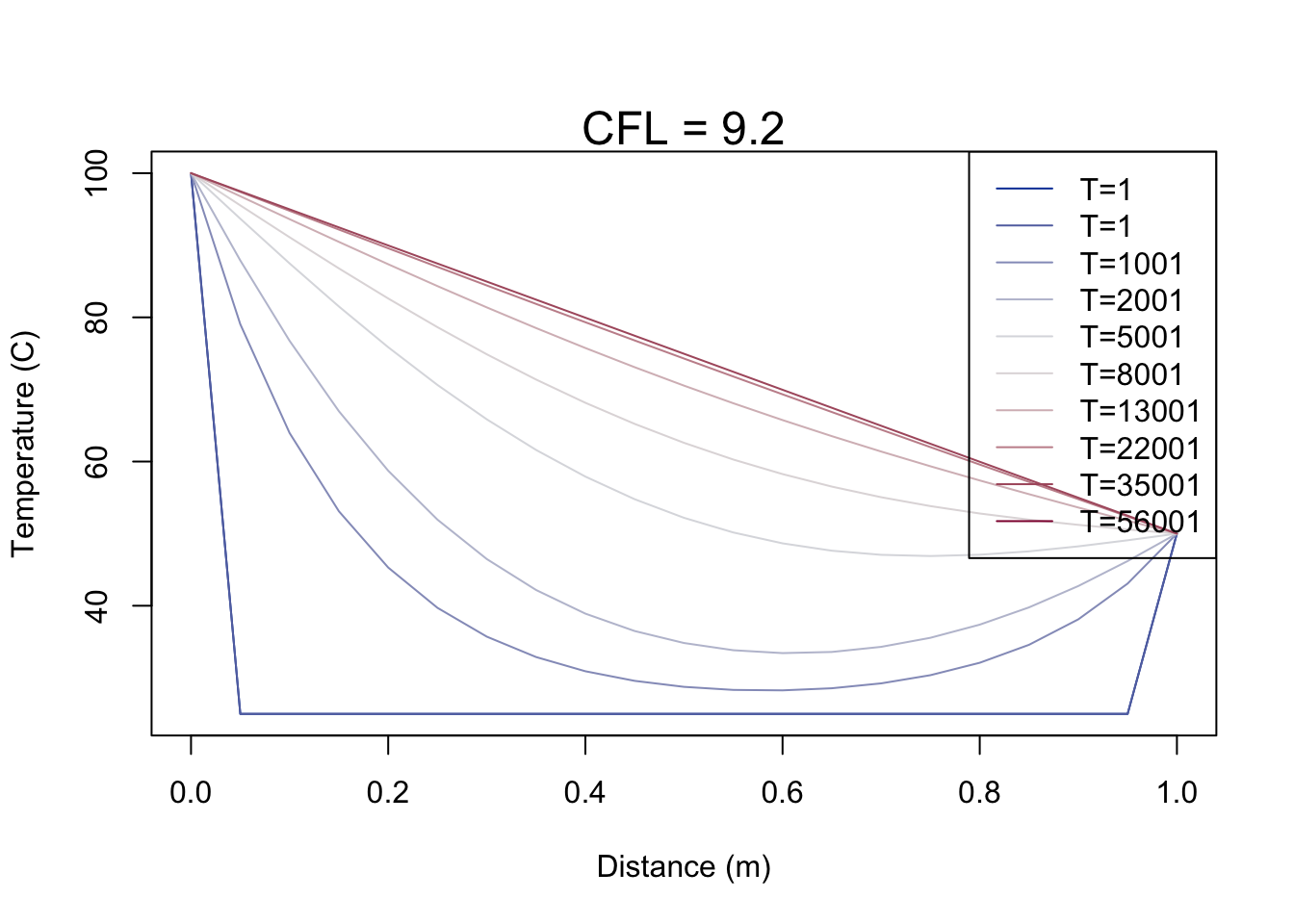

plot1(x, nout=10)

3.6.2 计算效率

source("Code/ch03/ch3_HeatTransferIm.R")
source("Code/ch03/ch3_HeatTransferEx.R")
Tmax = 1e4

t0 = Sys.time()
x=HT.explicit(DX= 0.025, DT = 5, U0=100, UL=50, uic = 25, X = 1, ignore.cfl=FALSE, plot=FALSE, Tmax=Tmax)

## [1] 0.184

t1 = Sys.time()
tu.ex = t1 - t0

t0 = Sys.time()
x=HT.implicit(DX= 0.025, DT = 5, U0=100, UL=50, uic = 25, X = 1, ignore.cfl=FALSE, plot=FALSE, Tmax=Tmax)

## [1] 0.184

t1 = Sys.time()
tu.im = t1 - t0

message('Time for implicit =', tu.im)

## Time for implicit =0.0979740619659424

message('Time for explicit =', tu.ex)

## Time for explicit =0.06929612159729

3.7 二维有限差分

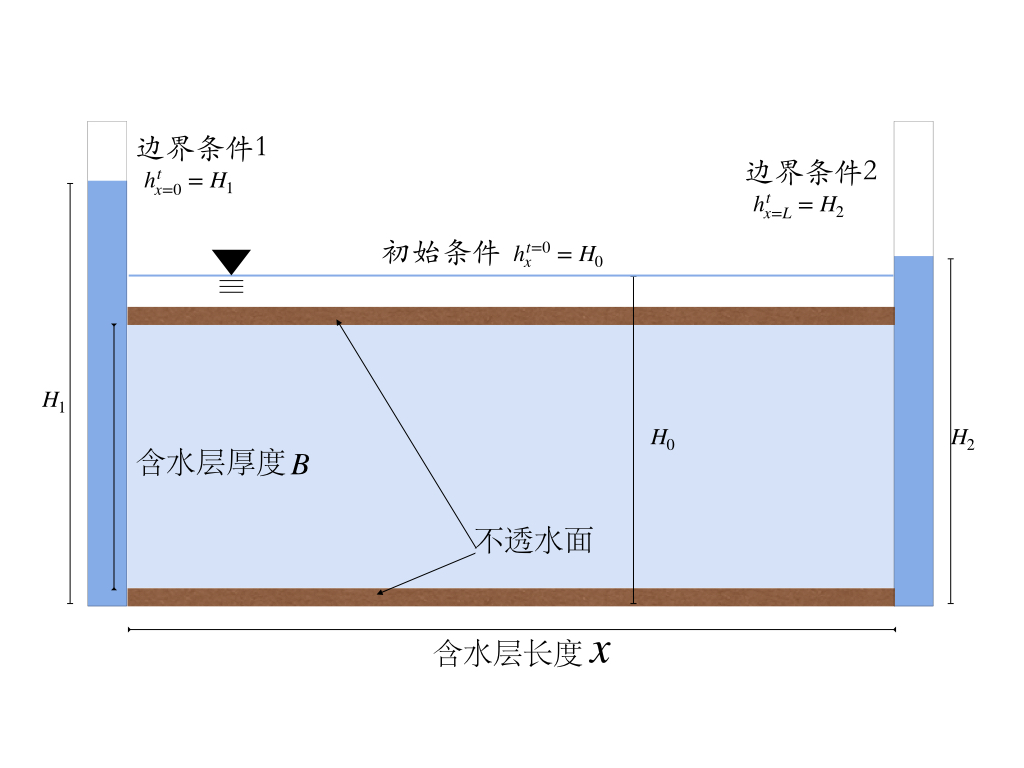
Example 3.2 sdhdt=kxB∗d2hdx2+kyB∗d2hdy2+ss

令Dx=kxBs和Dy=kyBs。

公式推导：

右边： ∂u∂t=ut+1i,j−uti,jΔt

左边：

Dx∂2u∂x2+Dy∂2u∂y2=Dxuti+1,j−2uti,j+uti−1,jΔx2+Dyuti,j+1−2uti,j+uti,j−1Δy2

控制方程离散化后得到： ut+1i,j−uti,jΔt=Dxuti+1,j−2uti,j+uti−1,jΔx2+Dyuti,j+1−2uti,j+uti,j−1Δy2

ut+1i,j−uti,j=DxΔtΔx2(uti+1,j−2uti,j+uti−1,j)+DxΔtΔy2(uti,j+1−2uti,j+uti,j−1)

令α=DxΔtΔx2, β=DxΔtΔy2, γ=1−2DxΔtΔx2−2DxΔtΔy2，公式变为：

ut+1i,j=αuti+1,j+βuti,j+1+γuti,j+βuti,j−1+αuti−1,j

二维离散化格点

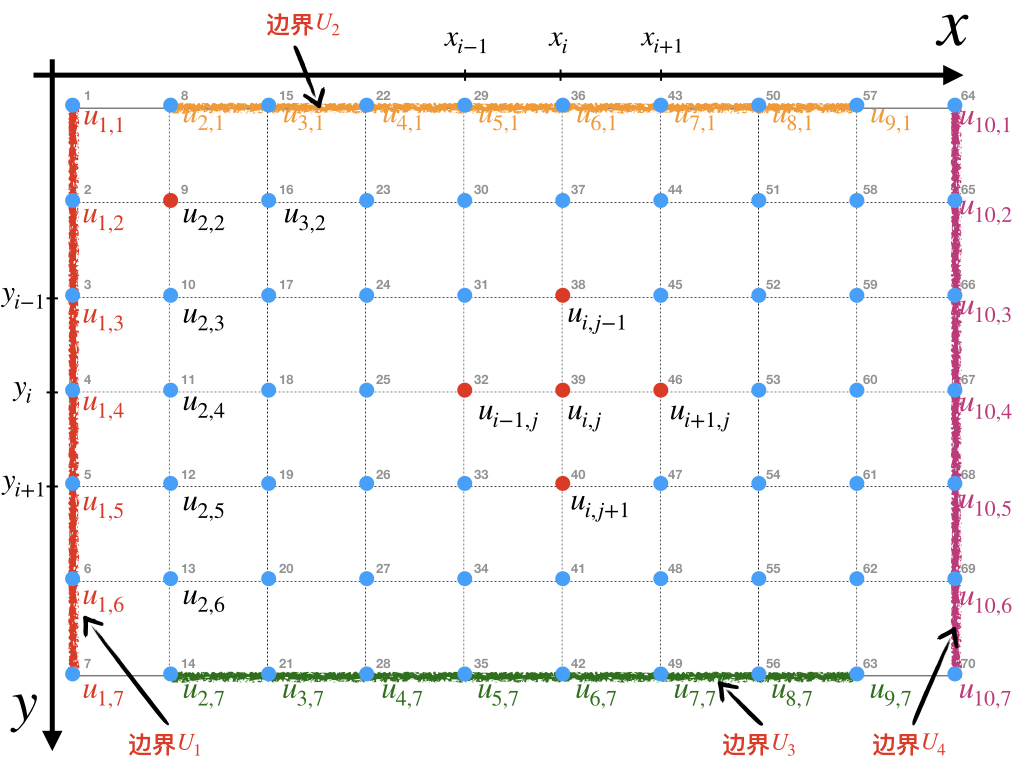
假设x和y方向总长为Lx和Ly，沿两个方向的离散点数为Nx=Lx/Δx, Ny=Ly/Δy, N=Nx∗Ny。 矩阵形式可表达为： x=A∗b

x=[[u1,1…u1,Ny][u2,1…u2,Ny]…ui,j…[uNx,1…uNx,Ny]]t

A=[[100010001]0000[1000000β…αγα…β0000001]0000[1000000β…αγα…β0000001]0000[100010001]]

b=[[U1]Ny∗1[U2u2,1…U3]Ny∗1[U2ui,j…U3]Ny∗1[U4]Ny∗1]t−1

3.7.1 编程求解

显式求解

#' Problem: 1D Confined Aquifer
#'  governing Eqn: du/dt = DDx * (dd u / d x^2) + DDy * (dd u / d y^2)
#'  
diag.matrix <- function(id = c(-1, 0, 1), x = rep(1, length(id)), n = 3, def.val = 0){
  val = matrix(x, ncol=length(id), nrow=1)
  mat = matrix(def.val, n, n)
  nid = length(id)
  for(i in 1:n){
    for(j in 1:n){
      for(k in 1:nid){
        if(i + id[k] == j){
          mat[i,j] = val[k]
        }
      }
    }
  }
  mat
}

toBC <- function(idl, x, val){
  nbc = length(idl)
  for(i in 1:nbc){
    x[idl[[i]]] = val[i]
  }
  x
}

CA.Explicit <- function(  bc1 = c(0, 0, 0,0),
                          bc2 = NULL,
                          uic = 25,
                          Lxy = c(1000, 1000),
                          Dxy = c(50,50),
                          DD = rep(23 ,2),
                          epsilon = 0.001,
                          DT = 25,
                          Tmax = 1e5,
                          ignore.cfl = FALSE, plot = TRUE){
  DX=Dxy[1]; DY=Dxy[2];
  tt = seq(0, Tmax, DT); 
  NT = length(tt)
  xx = seq(0, Lxy[1], DX); NX = length(xx)
  yy = seq(0, Lxy[2], DY); NY = length(yy)
  # NX = Lxy[1] / DX + 1;   NY = Lxy[2] / DY + 1
  N = NX * NY
  CFL.x = alpha = DD[1]  * DT / (DX * DX)
  CFL.y = beta  = DD[2]  * DT / (DY * DY)
  gamma = 1 - 2 * alpha - 2 * beta
  message('CFL value = (', CFL.x, '\t', CFL.y, ')')  
  if(!ignore.cfl){
    if(CFL.x >=.5 | CFL.y >=.5){
      stop()
    }
  }
  mat = diag.matrix(id = c(-NY, -1, 0, 1, NY), n=N,
                    x=c(alpha, beta, gamma, beta, alpha), def.val = 0)
  dmat = diag.matrix(id=0, x=1, n=N, def.val = 0)
  idl = list(1:NY,
             1+(1:NX - 1)*(NY),
             (1:NX) * NY,
             (NX-1)*(NY)+1:NY) 
  nbc = length(idl)
  id.bc = sort(unique(unlist(idl)))
  mat[id.bc, ] = dmat[id.bc,]
  
  arr = array(NA, dim=c(NY,NX,NT))
  # xm = matrix(NA, nrow=N, ncol=NT)
  vs = cbind(rep(0, N))
  # bc2=list(id=10, x=0.01)
  # vs[bc2$id] = bc2$x
  
  b=bx=cbind(rep(uic, N))
  b = toBC(idl = idl, x=b, val=bc1)
  
  for(i in 1:NT){
    if(i>1){
      bx = mat %*% b + vs * DT
      if(any(is.nan(bx))) { break }
      if(mean(abs(b-bx)) < epsilon) { break }
    }
    bx = toBC(idl = idl, x=bx, val=bc1)
    arr[, , i] = matrix(bx, nrow = NY, ncol = NX)
    b = bx
  }
  NT = i
  arr=arr[,, 1:NT]
  # message('Total Timesteps (dt * nt)= ', DT, ' * ', NT)
  # yy = arr; yy[abs(yy)>1e20] = NA
  ret = list('x' = xx,
             'y' = yy,
             'z' = arr,
             'time' = tt,
             'CFL' = c(CFL.x, CFL.y),
             'DT' = DT,
             'NT' = NT
  )
  return(ret)
}
plot.3d <- function(x, nr=3, nc=4, clim=NULL){
  par(mfrow=c(nr, nc), mar=c(1,1,1,1))
  idx = round(10^seq(0, log10(x$NT), length.out = nc*nr))
  z=x$z; 
  z[ is.infinite(abs(z)) ] = NA
  if(is.null(clim)){
    clim = range(z, na.rm = TRUE)
  }
  for(i in idx ){
    plot3D::persp3D(z=z[, , i], clim=clim,
            colvar=z[, , i])
    mtext(paste('T =', x$DT * i), side= 3, line=-1)
  }
}

library(plot3D)
source("Code/ch03/ch3_ConfAq2DIm.R")
x = CA.Explicit(bc1 = c(10, 30,10, 10),
                uic = 25,
                Lxy = c(1000, 1000),
                Dxy = c(50,50),
                DD = rep(23 ,2),
                epsilon = 0.001,
                DT = 25,
                Tmax = 1000
                )

## CFL value = (0.23    0.23)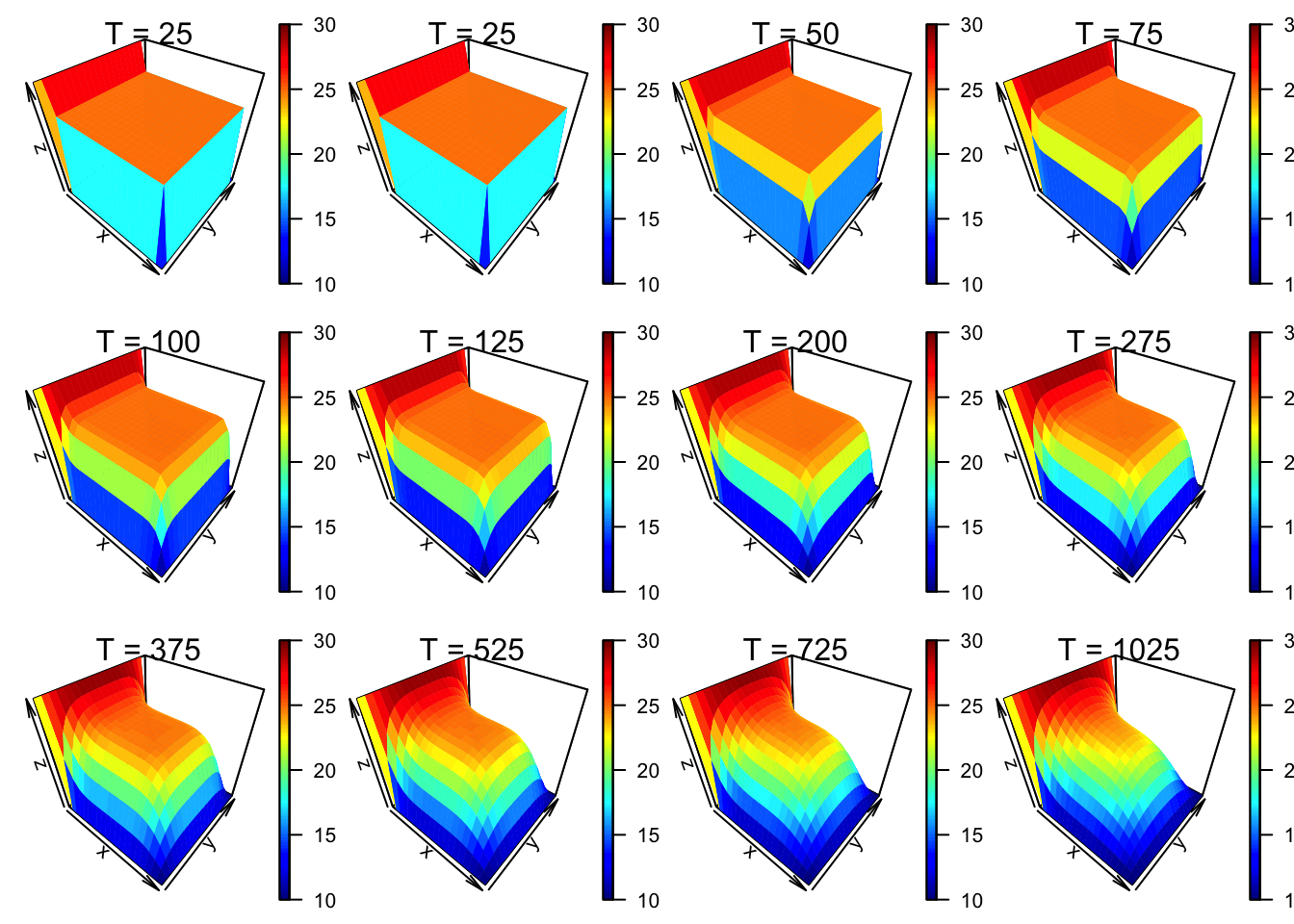

plot.3d(x)

隐式求解

#' Problem: 1D Confined Aquifer
#'  governing Eqn: du/dt = DDx * (dd u / d x^2) + DDy * (dd u / d y^2)
#'  
diag.matrix <- function(id = c(-1, 0, 1), x = rep(1, length(id)), n = 3, def.val = 0){
  val = matrix(x, ncol=length(id), nrow=1)
  mat = matrix(def.val, n, n)
  nid = length(id)
  for(i in 1:n){
    for(j in 1:n){
      for(k in 1:nid){
        if(i + id[k] == j){
          mat[i,j] = val[k]
        }
      }
    }
  }
  mat
}

toBC <- function(idl, x, val){
  nbc = length(idl)
  for(i in 1:nbc){
    x[idl[[i]]] = val[i]
  }
  x
}

CA.Implicit <- function(  bc1 = c(0, 0, 0,0),
                          bc2 = NULL,
                          uic = 25,
                          Lxy = c(1000, 1000),
                          Dxy = c(50,50),
                          DD = rep(23 ,2),
                          epsilon = 0.001,
                          DT = 25,
                          Tmax = 1e5,
                          ignore.cfl = FALSE, plot = TRUE){
  DX=Dxy[1]; DY=Dxy[2];
  tt = seq(0, Tmax, DT); 
  NT = length(tt)
  xx = seq(0, Lxy[1], DX); NX = length(xx)
  yy = seq(0, Lxy[2], DY); NY = length(yy)
  # NX = Lxy[1] / DX + 1;   NY = Lxy[2] / DY + 1
  N = NX * NY
  alpha = -DD[1]  * DT / (DX * DX)
  beta  = -DD[2]  * DT / (DY * DY)
  CFL.x =  DD[1]  * DT / (DX * DX)
  CFL.y =  DD[2]  * DT / (DY * DY)
  gamma = 1 + 2 * DD[1]  * DT / (DX * DX) + 2 * DD[2]  * DT / (DY * DY)
  message('CFL value = (', CFL.x, '\t', CFL.y, ')')  
  if(!ignore.cfl){
    if(CFL.x >=.5 | CFL.y >=.5){
      stop()
    }
  }
  #' =========================================
  x0 = rep(uic, NX)
  mat = diag.matrix(id = c(-NY, -1, 0, 1, NY), n=N,
                    x=c(alpha, beta, gamma, beta, alpha), def.val = 0)
  dmat = diag.matrix(id=0, x=1, n=N, def.val = 0)
  idl = list(1:NY,
             1+(1:NX - 1)*(NY),
             (1:NX) * NY,
             (NX-1)*(NY)+1:NY) 
  nbc = length(idl)
  id.bc = sort(unique(unlist(idl)))
  mat[id.bc, ] = dmat[id.bc,]
  
  arr = array(NA, dim=c(NY,NX,NT))
  vs = cbind(rep(0, N))
  b=bx=cbind(rep(uic, N))
  b = toBC(idl = idl, x=b, val=bc1)
  
  for(i in 1:NT){
    if(i>1){
      bx = solve(mat, b + vs * DT)
      if(any(is.nan(bx))) { break }
      if(mean(abs(b-bx)) < epsilon) { break }
    }
    bx = toBC(idl = idl, x=bx, val=bc1)
    arr[, , i] = matrix(bx, nrow = NY, ncol = NX)
    b = bx
  }
  NT = i
  arr=arr[,, 1:NT]
  # message('Total Timesteps (dt * nt)= ', DT, ' * ', NT)
  # yy = arr; yy[abs(yy)>1e20] = NA
  ret = list('x' = xx,
             'y' = yy,
             'z' = arr,
             'time' = tt,
             'CFL' = c(CFL.x, CFL.y),
             'DT' = DT,
             'NT' = NT
  )
  return(ret)
}
plot.3d <- function(x, nr=3, nc=4, clim=NULL){
  par(mfrow=c(nr, nc), mar=c(1,1,1,1))
  idx = round(10^seq(0, log10(x$NT), length.out = nc*nr))
  z=x$z; 
  z[ is.infinite(abs(z)) ] = NA
  if(is.null(clim)){
    clim = range(z, na.rm = TRUE)
  }
  for(i in idx ){
    plot3D::persp3D(z=z[, , i], clim=clim,
            colvar=z[, , i])
    mtext(paste('T =', x$DT * i), side= 3, line=-1)
  }
}

library(plot3D)
source("Code/ch03/ch3_ConfAq2DIm.R")
x = CA.Implicit(bc1 = c(10, 30,10, 10),
                uic = 25,
                Lxy = c(1000, 1000),
                Dxy = c(50,50),
                DD = rep(23 ,2),
                epsilon = 0.001,
                DT = 25,
                Tmax = 1000
                )

## CFL value = (0.23    0.23)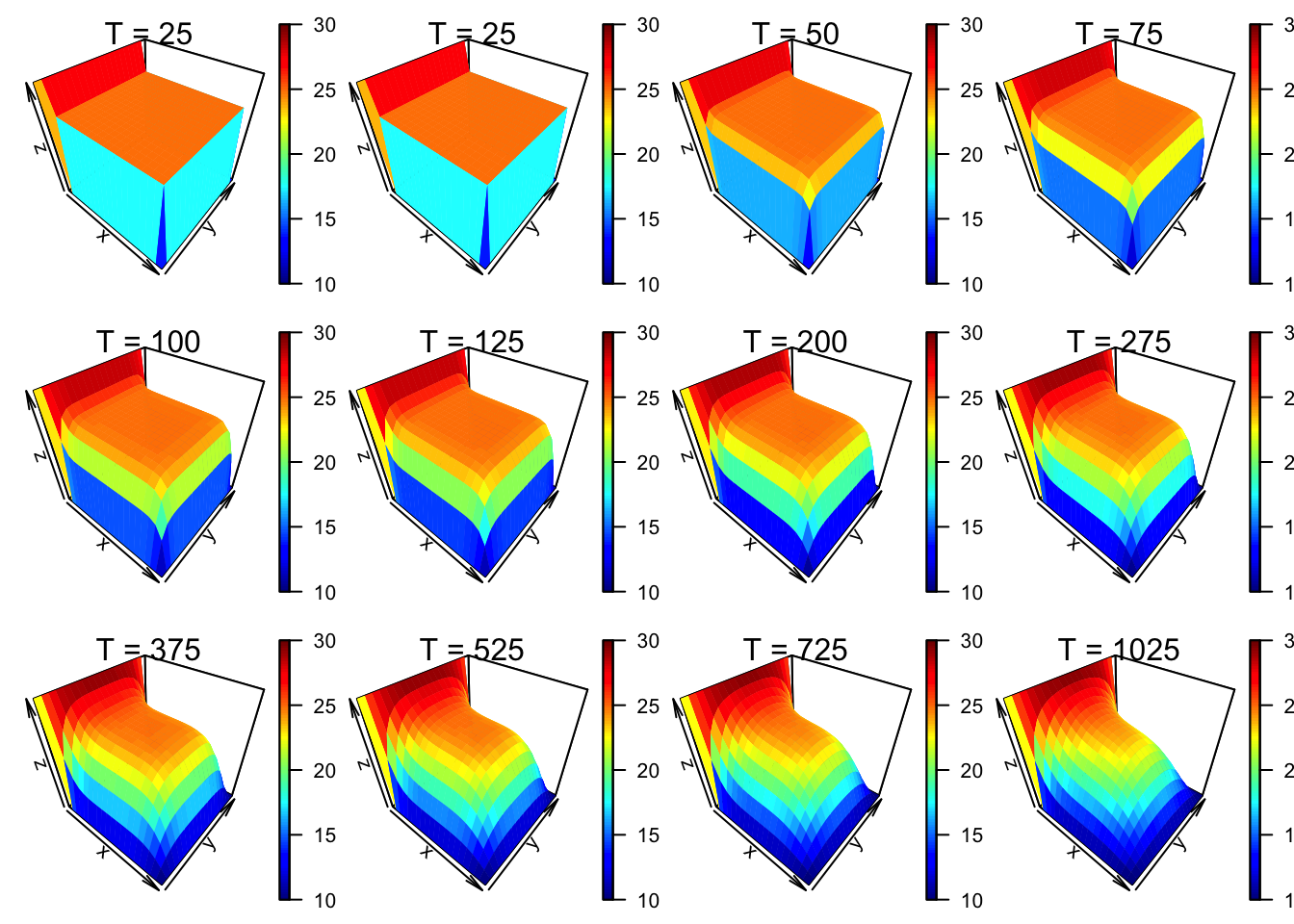

plot.3d(x)

对比隐式与显式求解法的时间步长和效率：

rm(list=ls())
library(plot3D)
source("Code/ch03/ch3_ConfAq2DEx.R")
source("Code/ch03/ch3_ConfAq2DIm.R")
Tmax = 1e4
dx = dy = 50
t0 = Sys.time()
x1 = CA.Explicit(Tmax = Tmax, DT = 25, 
                 Lxy = c(1000, 1000), Dxy = c(dx, dy),
                 ignore.cfl = TRUE)

## CFL value = (0.23    0.23)

t1 = Sys.time()
tu.ex = t1 - t0

t0 = Sys.time()
x2 = CA.Implicit(Tmax = Tmax, DT = 25, 
                 Lxy = c(1000, 1000), Dxy = c(dx, dy),
                 ignore.cfl = TRUE)

## CFL value = (0.23    0.23)

t1 = Sys.time()
tu.im = t1 - t0

df = data.frame( 'Type' = c('Explicit', 'Implicit'),
                 'NT' = c(x1$NT, x2$NT), 
                 'DT' = c(x1$DT, x2$DT),
                 'Time' = c(tu.ex, tu.im),
                 'CFL.X' = c(x1$CFL[1], x2$CFL[1]),
                 'CFL.Y' = c(x1$CFL[2], x2$CFL[2])
)
print(df)

##       Type  NT DT          Time CFL.X CFL.Y
## 1 Explicit 401 25 3.523902 secs  0.23  0.23
## 2 Implicit 401 25 7.618441 secs  0.23  0.23